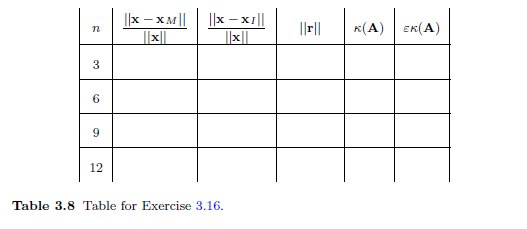
3.16. This problem considers two ways to solve Ax - b, where A is an n x n magic matrix and the exact solution is x = (1,1, 1)T. The matrix A should be calculated in MATLAB using the magic(n) command, and calculate b using the formula b = Ax. In what follows XM designates the solution computed using the MATLAB backslash operator, and xr is the solution computed using the inverse formula XI = A-lb. Use MATLAB to fill out Table 3.8 and then answer the following questions (note that r - b- AxM). Also, the entries in the table only need to include two significant digits, and the norms refer to the infinity norm (a) Do you see any substantial differences between the two solution methods when they are compared using the relative error? (b) Does a small residual indicate an accurate solution? Your answer should include a comment on the value of the condition number. What about any dependence on the size n of the matrix? (c) How well does the last column predict the relative error