Question: 32. In each case, graph a smooth curve whose slope meets the condition. a. Everywhere positive and increasing gradually. b. Everywhere positive and decreasing gradually.

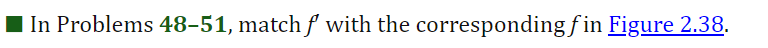
![decreasing gradually. c. Everywhere negative and increasing gradually [becoming less negative]. d.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666538768c78f_6226665387675d58.jpg)
![Everywhere negative and decreasing gradually [becoming more negative]. \fIn the graph shown](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66653876c9d38_62266653876b155a.jpg)

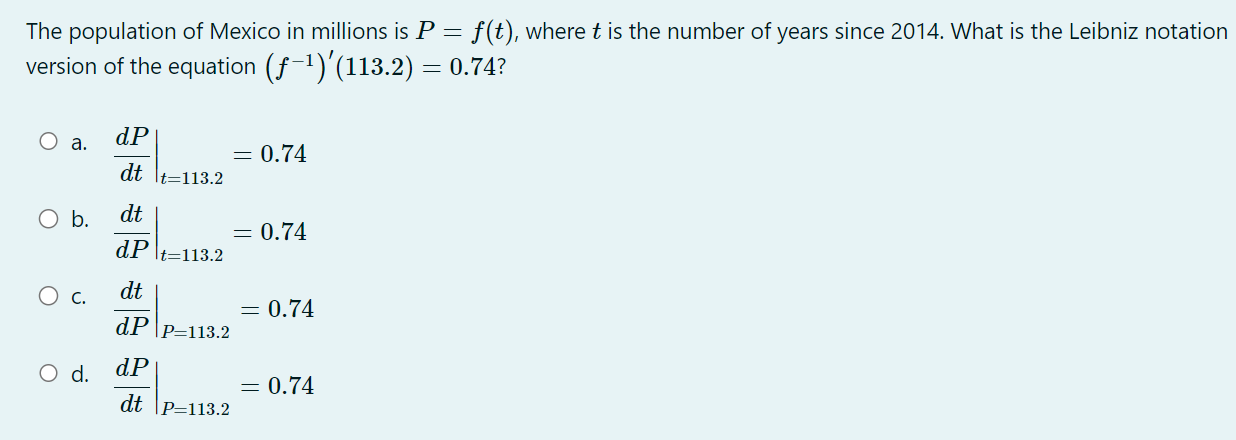
![to a: : :35 (over the intervals [0, 3:2] and [$4, 335]).](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665387856ca1_6246665387841af7.jpg)
![interval [2:1, 322]}. O c. Froma: 0 to :1: : 3:1 and](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666538791fde7_6256665387901ed0.jpg)
![from :1: : 3:4 to m : 3:5 (overthe intervals [0, 3:1]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666538797eb29_6256665387964352.jpg)
![and [$4, 315]). 0 d. From a: : $1 to :1: :](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66653879da15f_62566653879bda9e.jpg)
![3:3 (over the interval [3:1, 3:3]). The population of Mexico in millions](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665387a43705_6266665387a2201d.jpg)
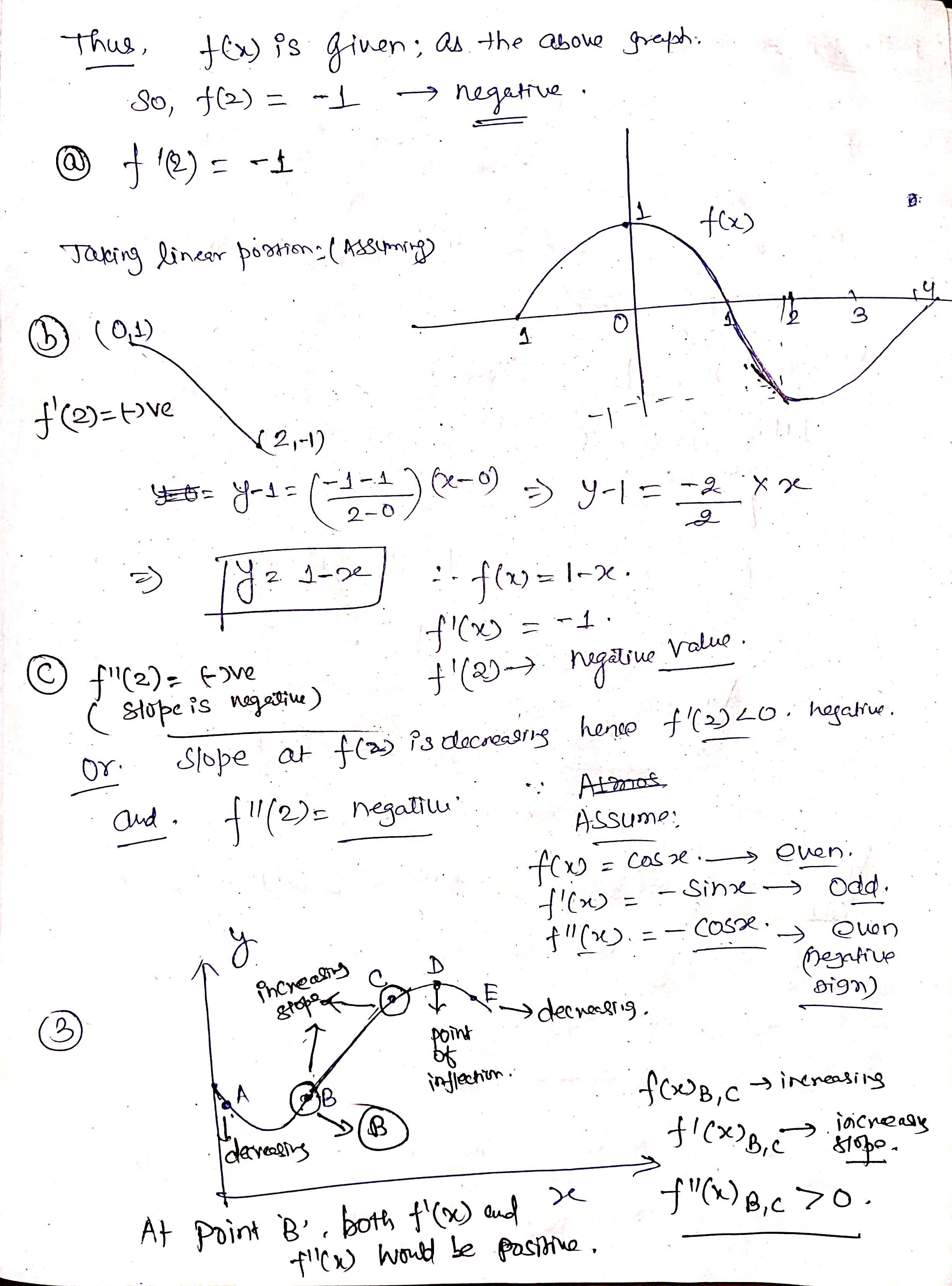

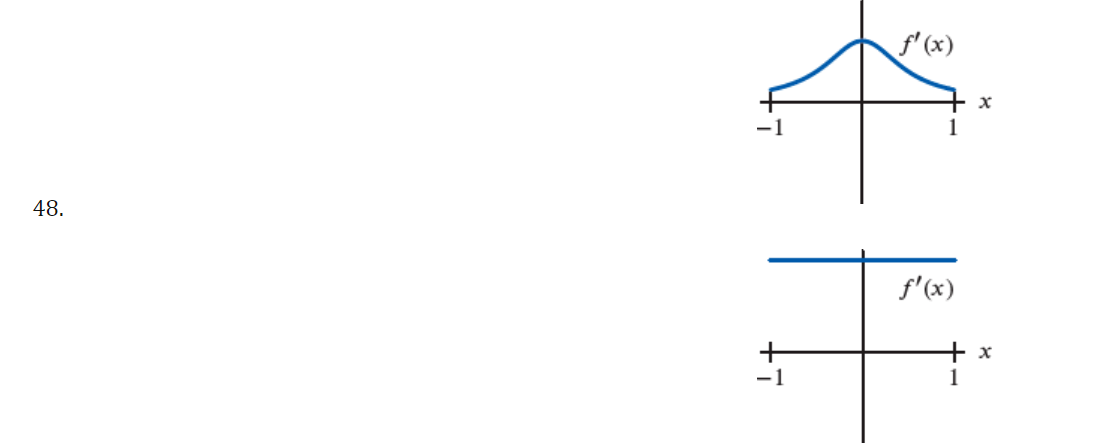
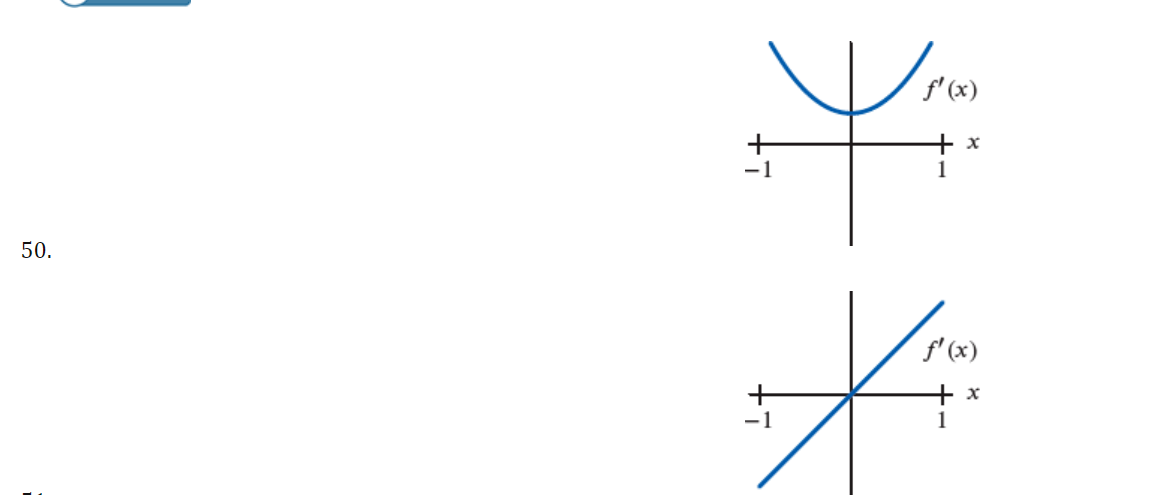
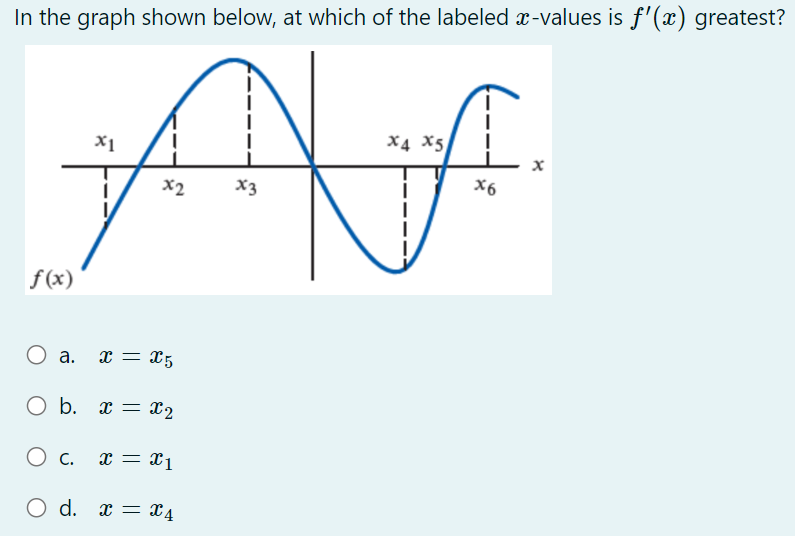

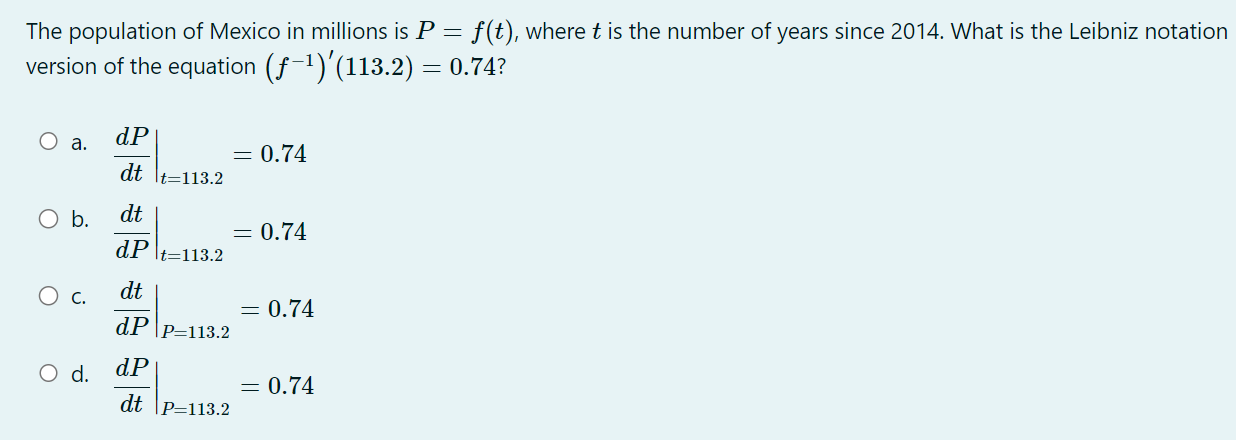
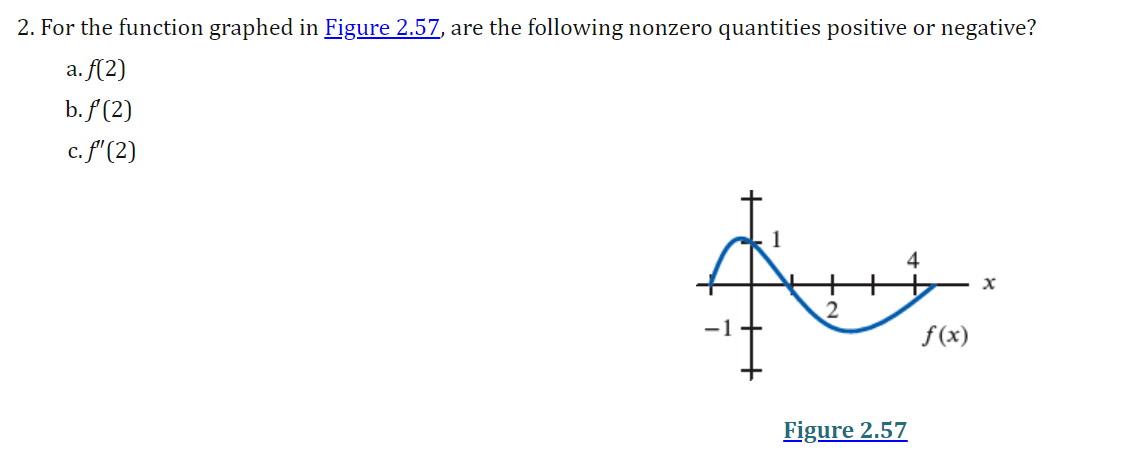
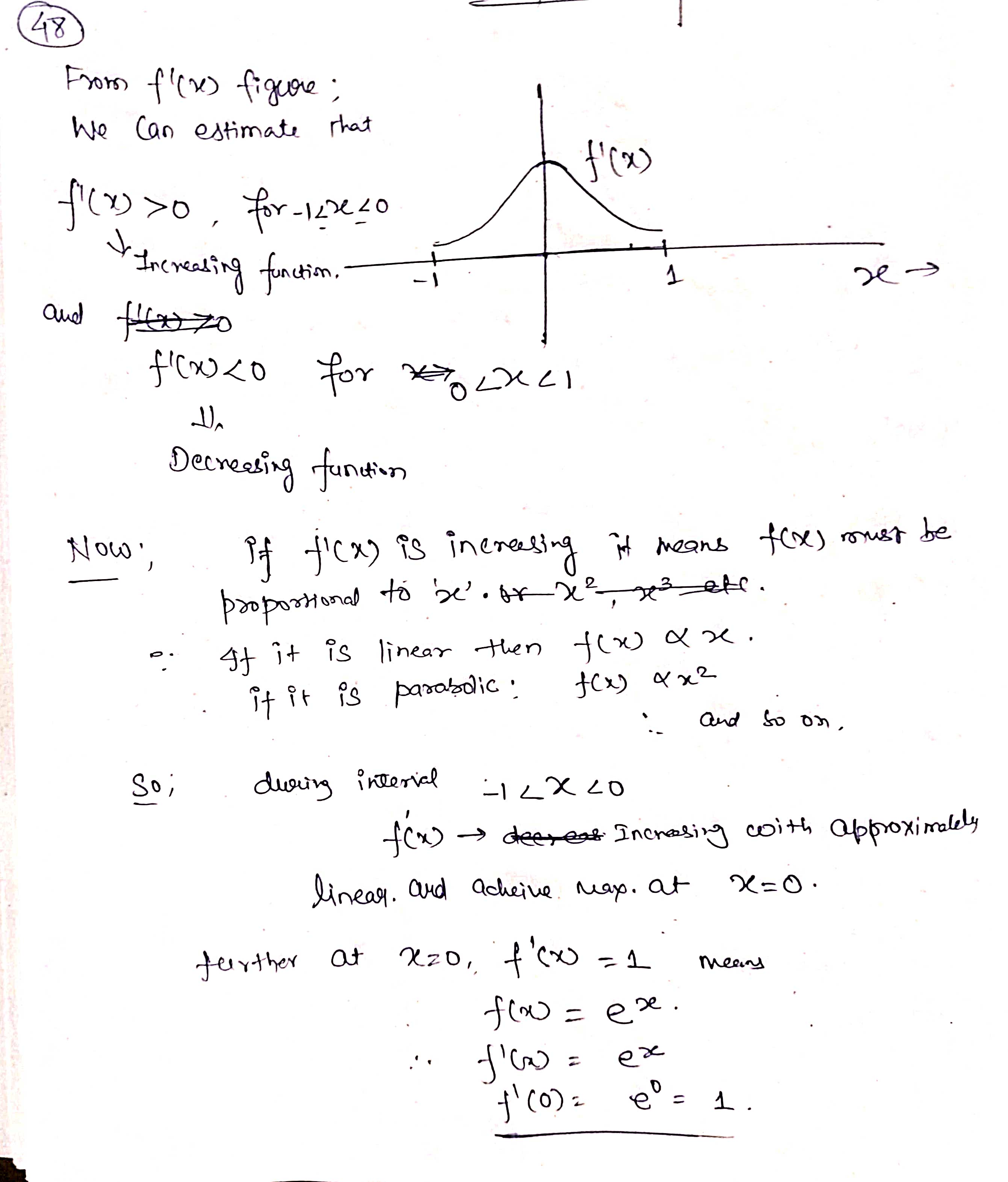
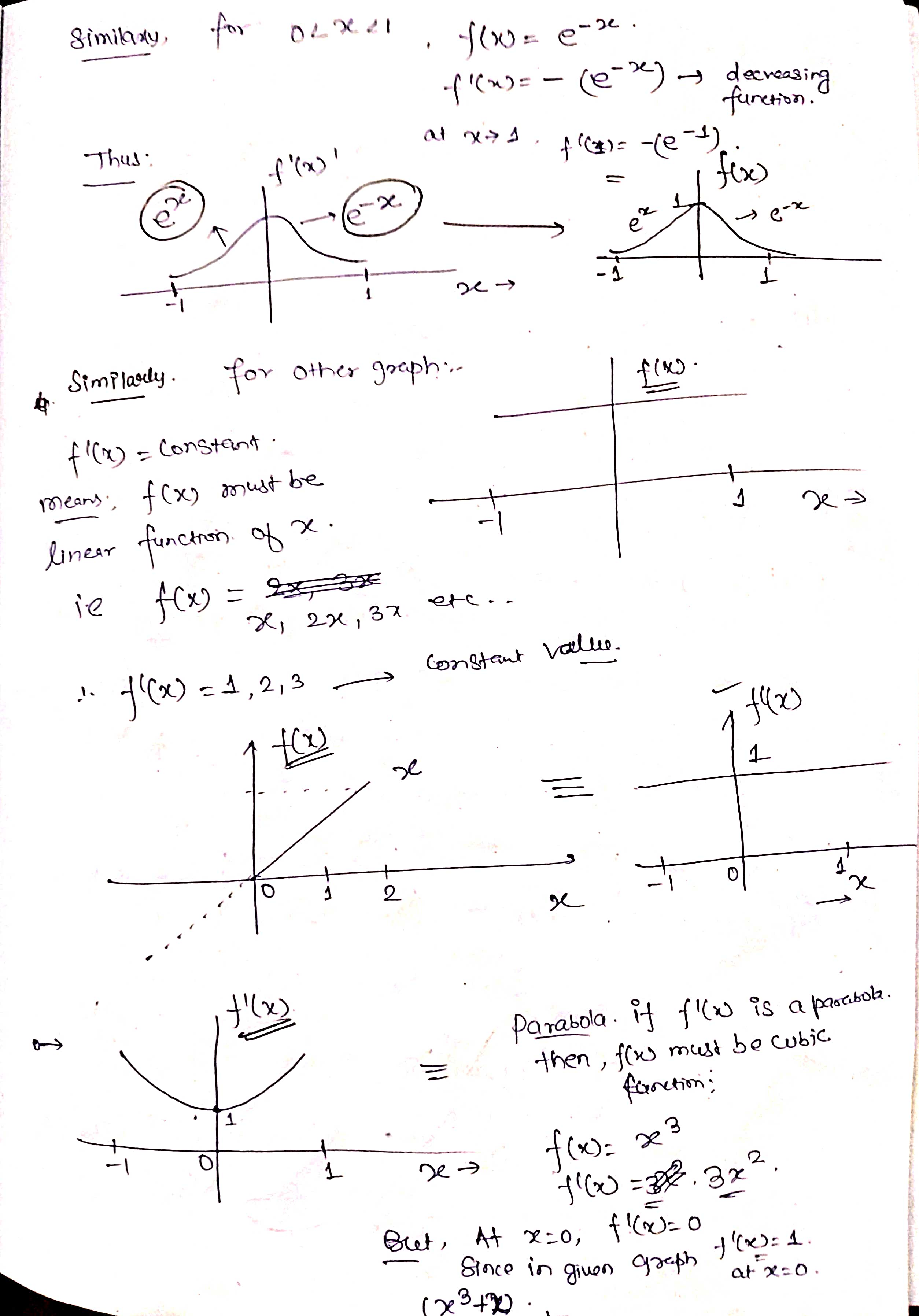
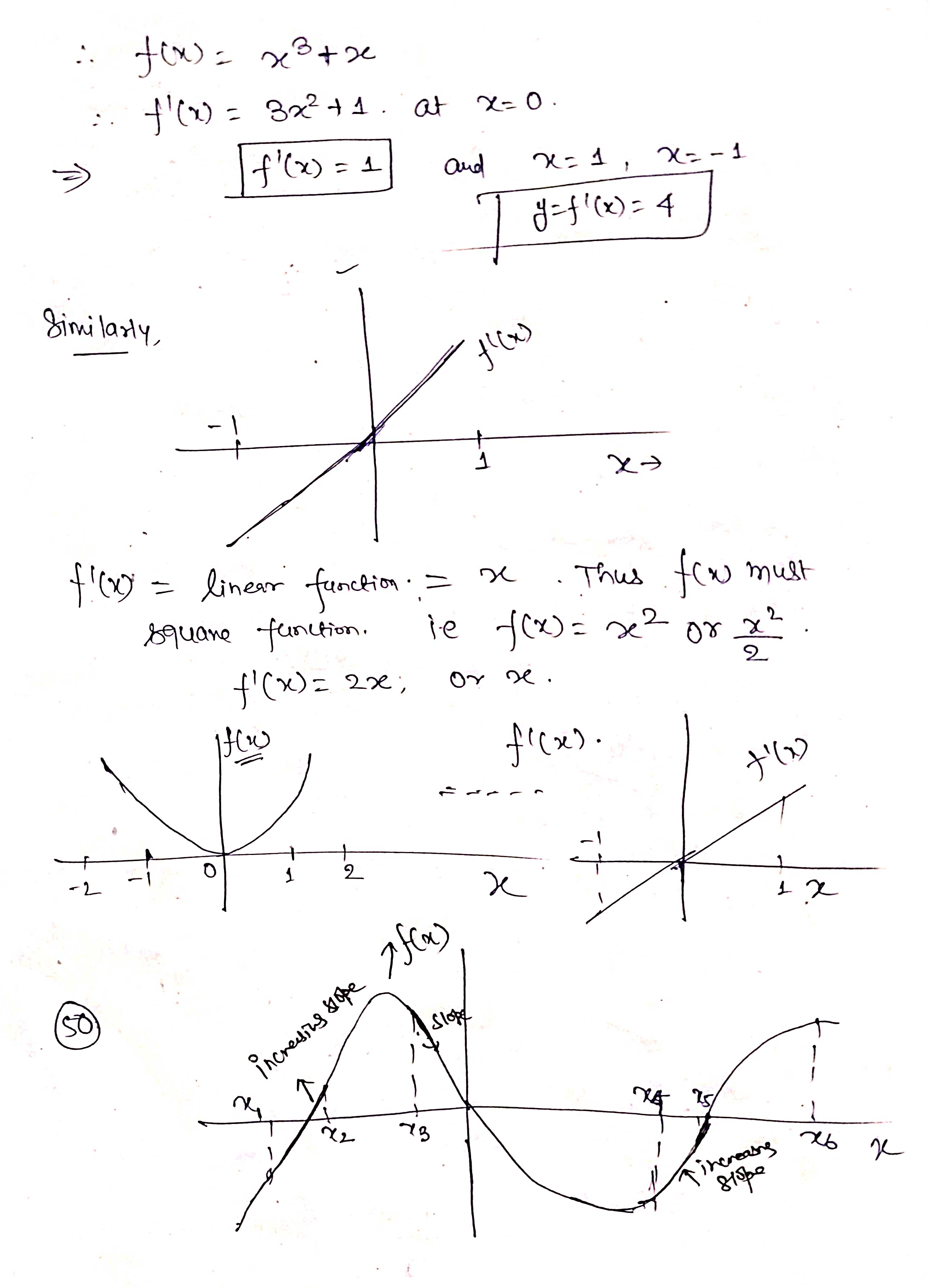
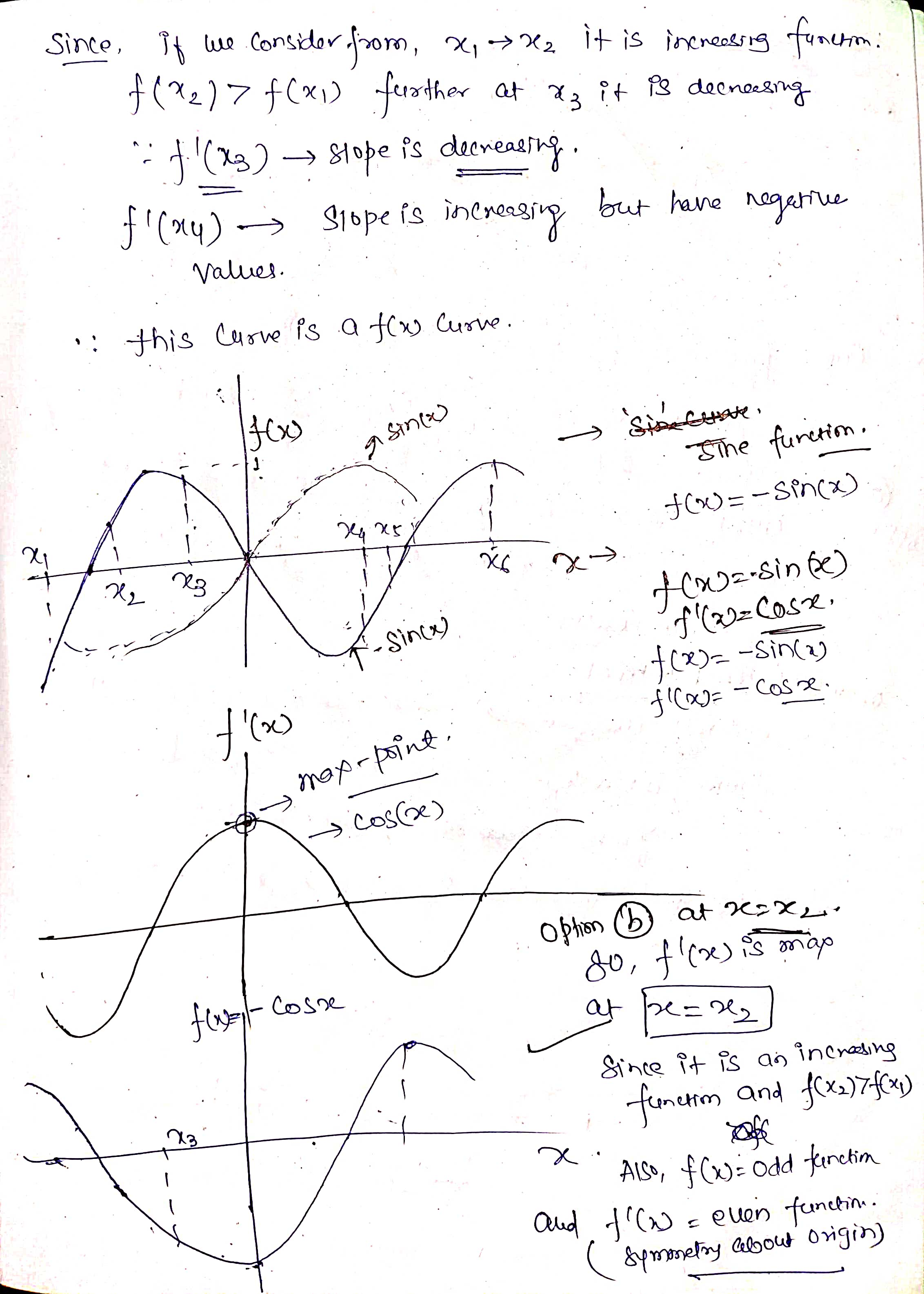

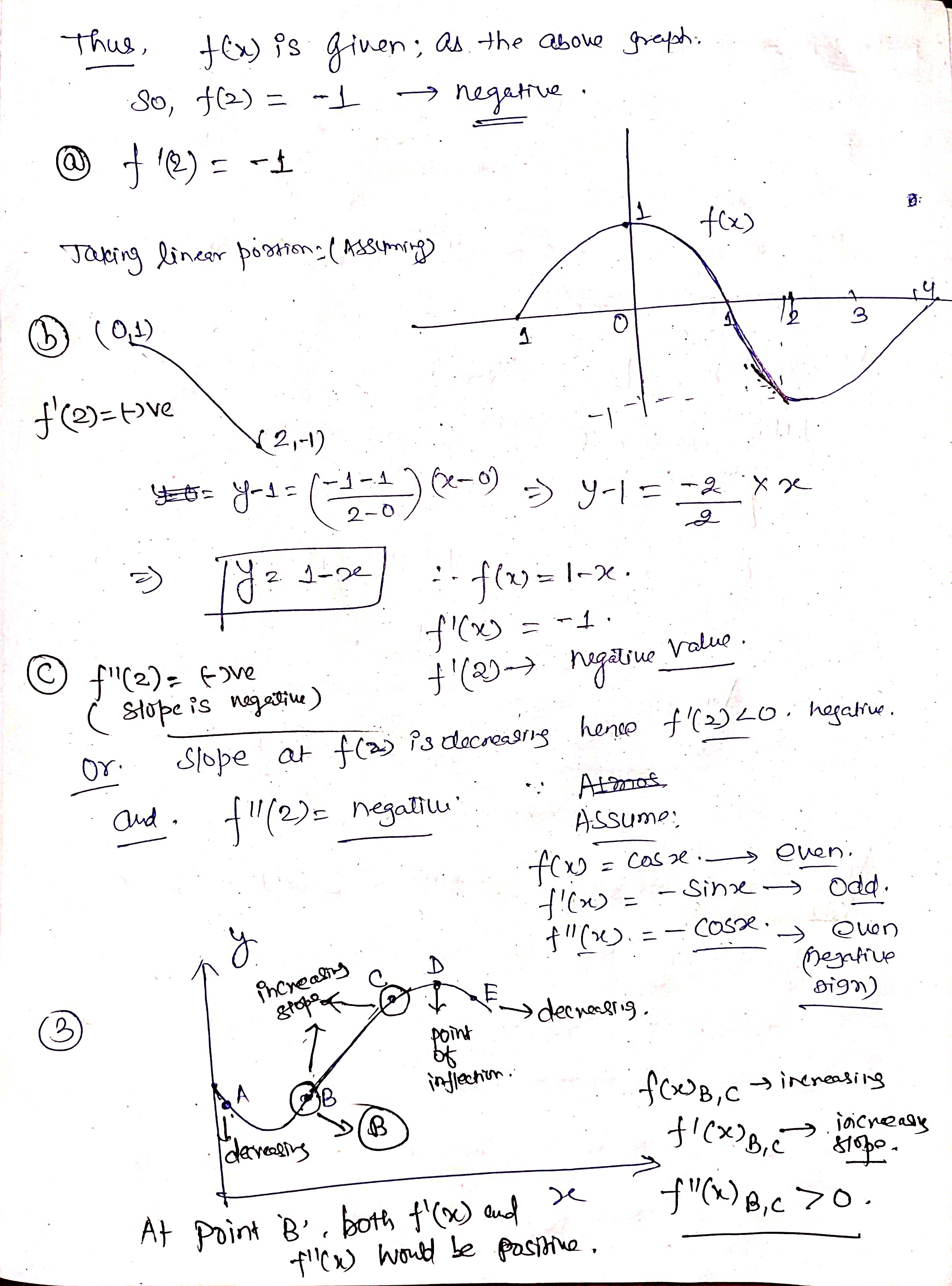
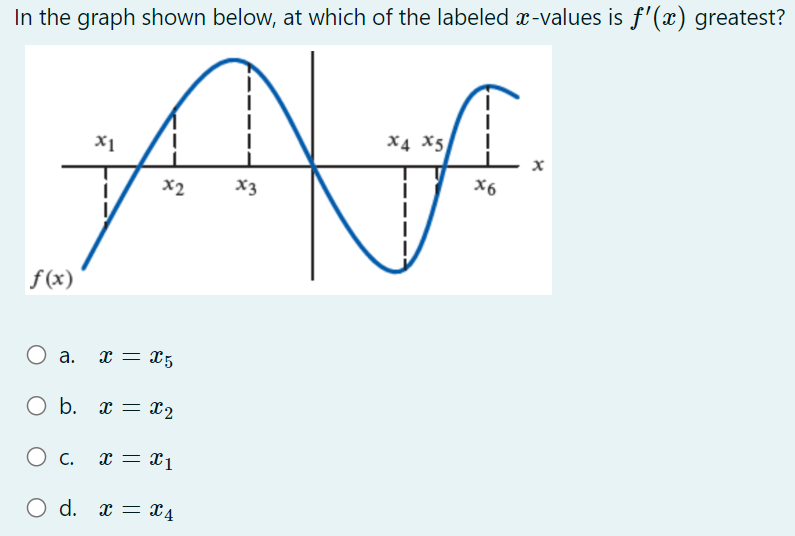
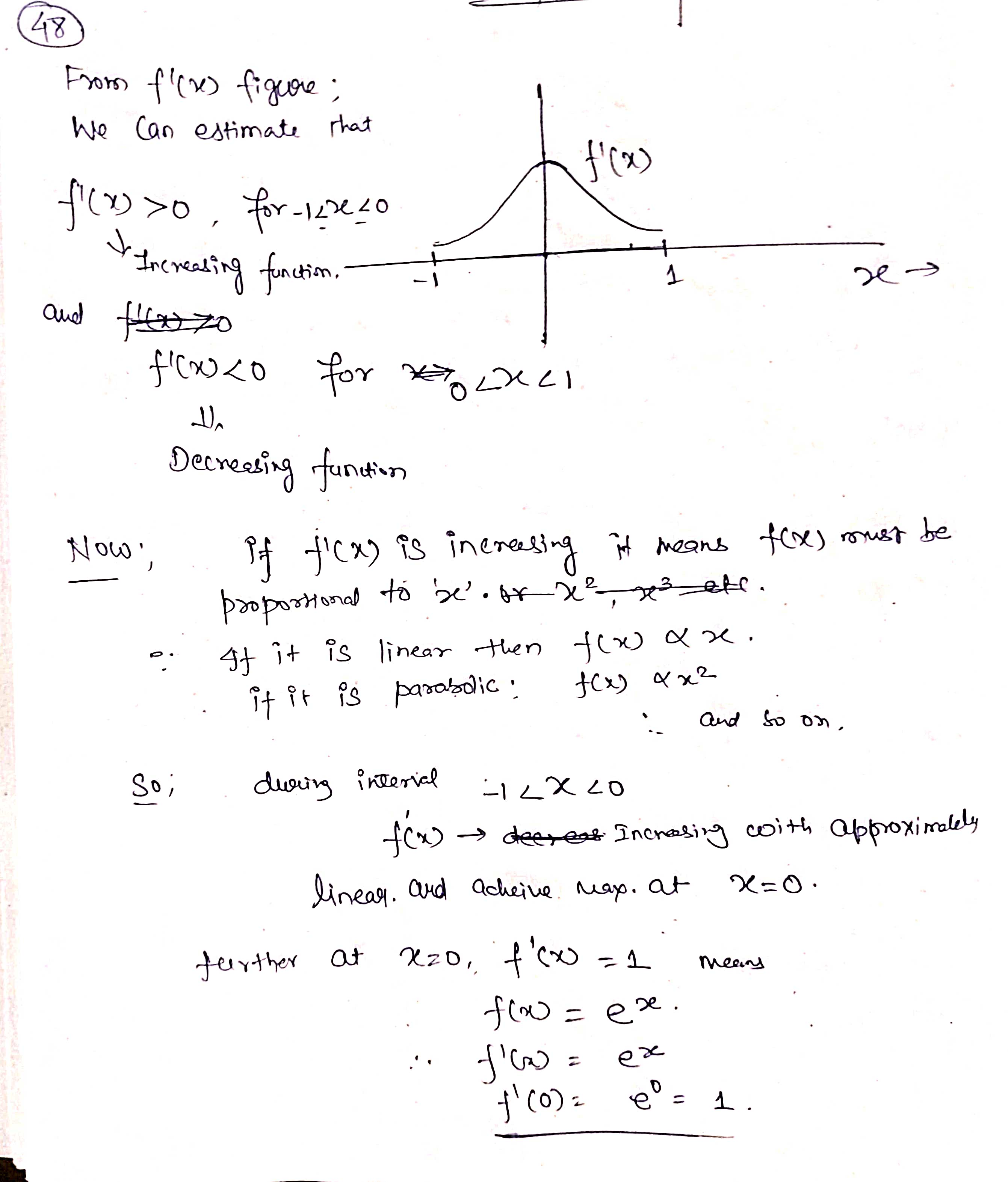
32. In each case, graph a smooth curve whose slope meets the condition. a. Everywhere positive and increasing gradually. b. Everywhere positive and decreasing gradually. c. Everywhere negative and increasing gradually [becoming less negative]. d. Everywhere negative and decreasing gradually [becoming more negative]. \fIn the graph shown below, at which of the labeled zitvalues is f'(a:) greatest? The graph shown below is the graph of the derivative 3\" of some function f. On which interval{s) is the function f increasing? 0 a. From a: : 0 to :r: : 3:2 and from x : 3:4 to a: : :35 (over the intervals [0, 3:2] and [$4, 335]). O b. From :3 : 3:1 to :1: : :32 (over the interval [2:1, 322]}. O c. Froma: 0 to :1: : 3:1 and from :1: : 3:4 to m : 3:5 (overthe intervals [0, 3:1] and [$4, 315]). 0 d. From a: : $1 to :1: : 3:3 (over the interval [3:1, 3:3]). The population of Mexico in millions is P = f(t), where t is the number of years since 2014. What is the Leibniz notation version of the equation (f-1) (113.2) = 0.74? O a. dp = 0.74 dt It=113.2 O b. dt = 0.74 dP It=113.2 O c. dt = 0.74 dP p-113.2 O d . dp = 0.74 dt p-113.22. For the function graphed in Figure 2.57, are the following nonzero quantities positive or negative? a. f(2) b. f (2 ) c. f' (2) 4 X 2 f (x) Figure 2.573. At one of the labeled points on the graph in Figure 2.58 both dy/dx and day/ dx are positive. Which is it? C D E A B X Figure 2.5848 From flexes figure : We can estimate that f' ( x ) fi( x) >o, for-12x40 * Increasing function . 1 and fieszo for LXLI Decreasing function Now . if ficx ) is increasing it means f(x ) must be proportional to be'. or x2 3 off. If it is linear then f( x) xx . if it is parabolic . J ( x ) 4 x2 and to on . So ; during interial -12X 20 f( x ) - Increasing with approximately linear . and Acheine Max . at X=0 . further at x20 , f'(x) = 1 means flo = ex . J' (x) = ex f' ( 0 ) = e = 1 .Similady, for 02X21 - ( ' ( x) = - ( 2- 3 ) - decreasing Thus : function . at x9 4 . "(Ca)= - ( e - 3 ) 5 - e-x Similarly . for other graph . f (x ) = constant . means . f (x) must be linear function of x . ie f( x) = 28, X, 22, 37 etc .. 1. {( ( x ) = 4 , 2 , 3 . constant vallee . H( x ) 1 f ( x) De 1 O + 2 x f' ( x ) Parabola . if film is a parabola . then , fox) must be cubic. 1 function : O 1 f ( x ) = 23 10 = 32. 3x2. But , At 2= 0 , f 1 ( x ) - 0 Since in given graph J ( x )= 1 at x=0: J ( x ) = 3+ ze :. f' ( x ) = 3x2+1 . at x- 0. f' ( x ) = 1 and X=1 , X - - 1 [ i f ' ( x) = 4 Similarly, +' ( x) fi(x ) = linear function . = 2 . Thus few must Square function . ie f(x) = ze 2 0x x 2 f' (x ) = 2x ; or re . 2 ficx ) . f' ( x) 2 SO increasing slope 7 f ( x ) Slope x xb increasing 81speSince , if we consider . from , 2 , -22 it is increasing funcrim : f ( x2 ) 7 f ( x 1) further at 2 3 it is decreasing " 41( x3 ) - slope is decreasing fi(my ) - slope is increasing but have negative values. . : this Curve is a fox curve. - SThe function . J ( x ) = - sin(x ) x6 . (x) = sin fe ) 7- Sin(x ) f ( 2) = COST , f. ( x ) = - sin (2) fix) = = cosse. may-point. -> Cos ( e ) Option (b) at rezx 2. fiE - Cosse so , f ( x ) is map at re = 212 Since it is an increasing X3 function and f ( x 2 ) 7 f( x , ) X " Also , f( x)= odd functim and J'(20 = even functin . ( Symonetry about origin )fl x4 nes Given function is f ' function ( derivative ) 80 , during interval ze, to x 2. f' is increasing a function Slope is increasing . option during $. x2-to x4 if is decreasing ( slope deereales from xy to agr slope increases . ophin @) is correct statement . So , entirely we can say that function f' is increasing from interval . x= 0 to me = x2 and from x - xy to x = zer Over the interval of foxz] and ( sy,x5 ) of f( x ) 3 4Thus , fox) is given ; as the above greysh. So, f( 2 ) = - 1 negative @ ( 1( 2 ) = - 1 Taking linear postions ( Assuming f( x ) 3 f ( 2 ) = tive ( 2 , -1 ) 40 = 4-1 = - 1 -1 (e - 0) 2 - 0 = ) y- 1 = - 2 x x 2 :- f ( x) = Inx . f'(x ) = - 1 . C f" ( 2 ) = Five J' (21 -) negative value . Slope is negative ) or . Slope at f(2) is decreerig hence f'(2)20 . hegatrue .' and . ( 1/ ( 2 ) = negatill ' Atmof Assume : fox = cosse . even, J'(x) = - since - odd. $" (x). = - cosse. - Quen increating negative 3 I decreasing . Dign ) point OK A B inflection . SO B, C increasing B decreeling f ' ( x ) Bic lacreally At Point B' , both f' ( ) and be f" ( x ) B , C 70 . " (x ) would be positive
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


