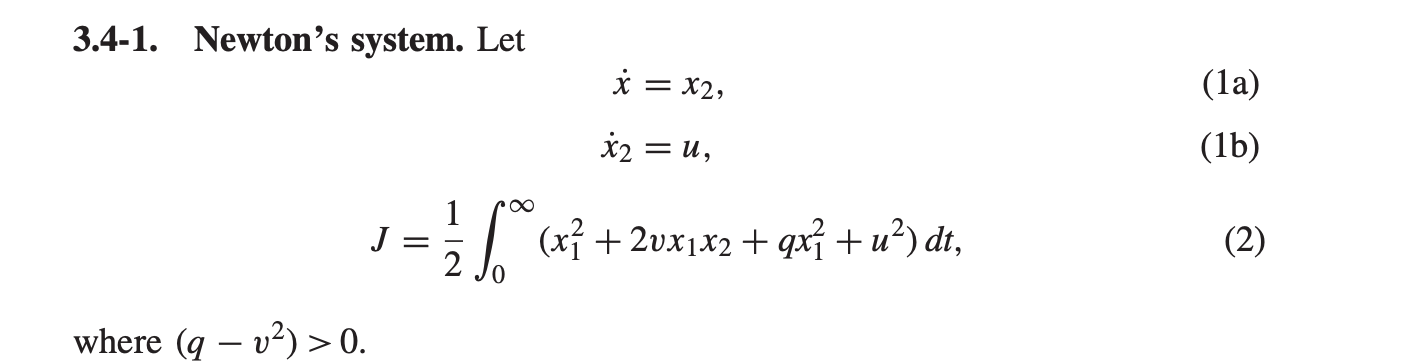
3.4-1. Newton's system. Let where (q v) > 0. J x = x2, x2 = U, = 1/2 (x + 2vx1x2 + qx + u) dt, (la) (1b) (2) 4.1-2. Design a tracker for the system in Problem 3.4-1. It is desired that x(t) track a reference signal r(t). Let weights q = 10, r = 1. a. Find the system for generating the command input v(t). b. If r(t) = u_(t), the unit step, solve for v(t). Now solve for the closed-loop state trajectory if x (0): = 0. c. Solution for the finite horizon control on [0, T] is more difficult; however, write subroutines in MATLAB to solve and simulate the tracking problem. Simulate also the case when x(0) = [1_0], r(t) = u1(t 1).