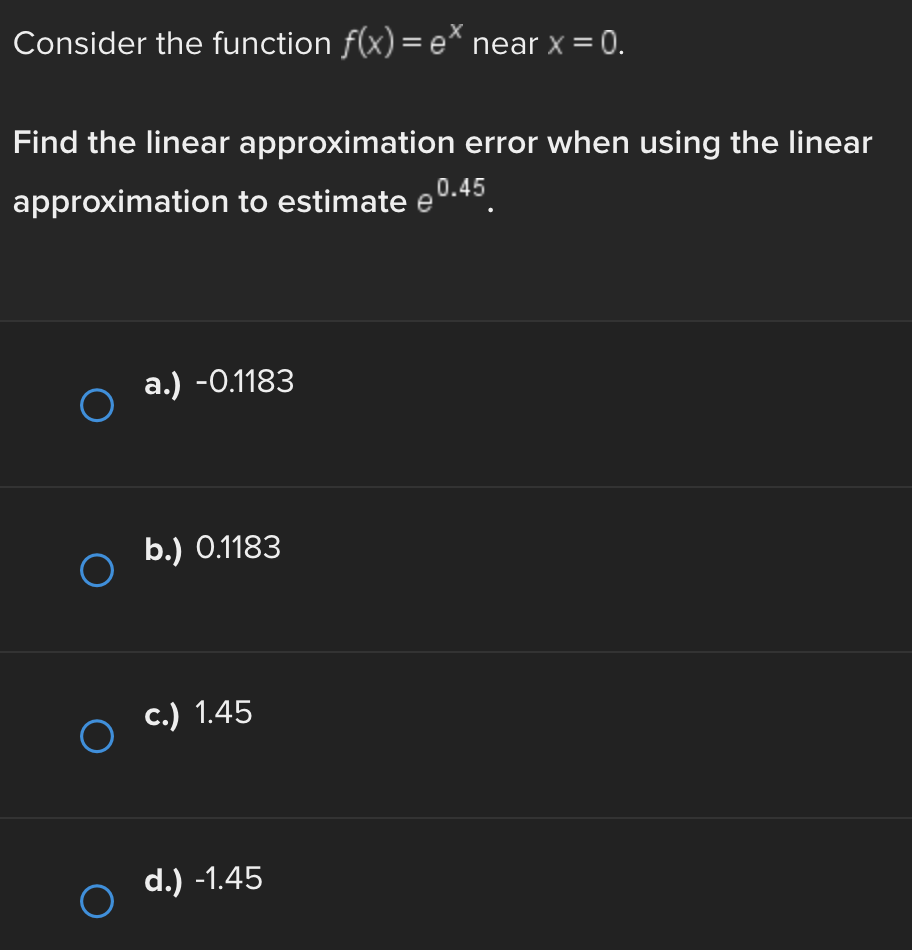
Question: 3/4/2 Consider the function f(x) = e* near x = 0. Find the linear approximation error when using the linear approximation to estimate e 0-45





3/4/2
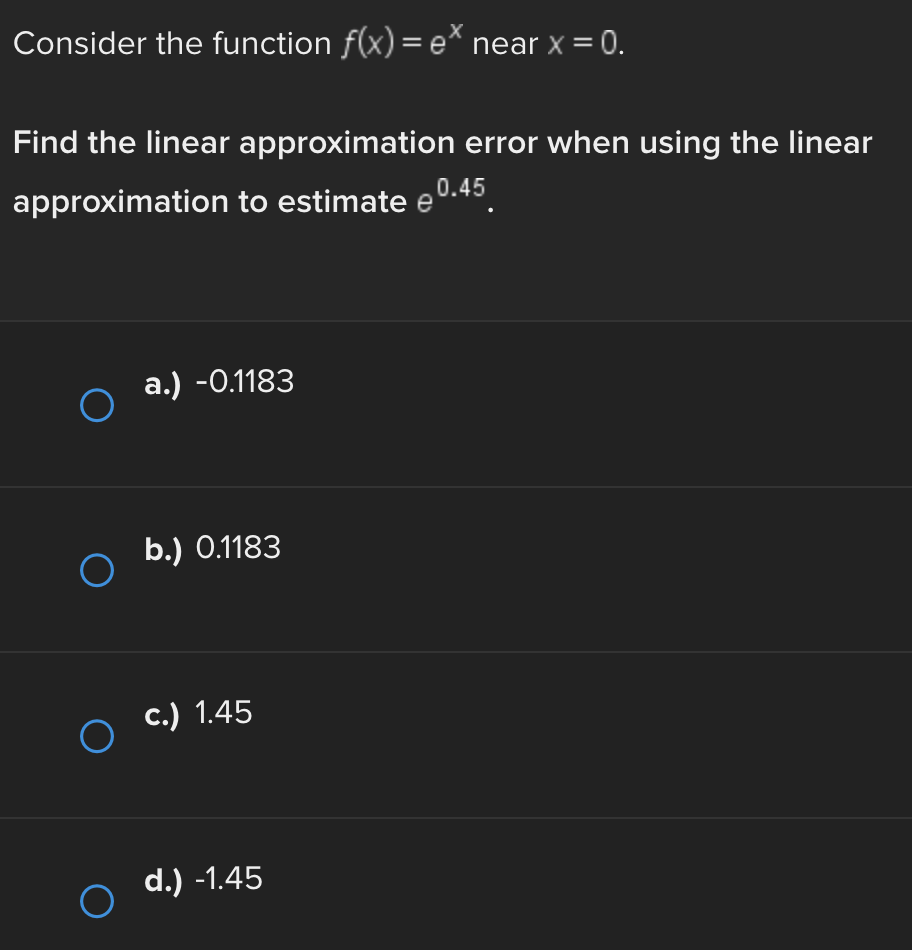
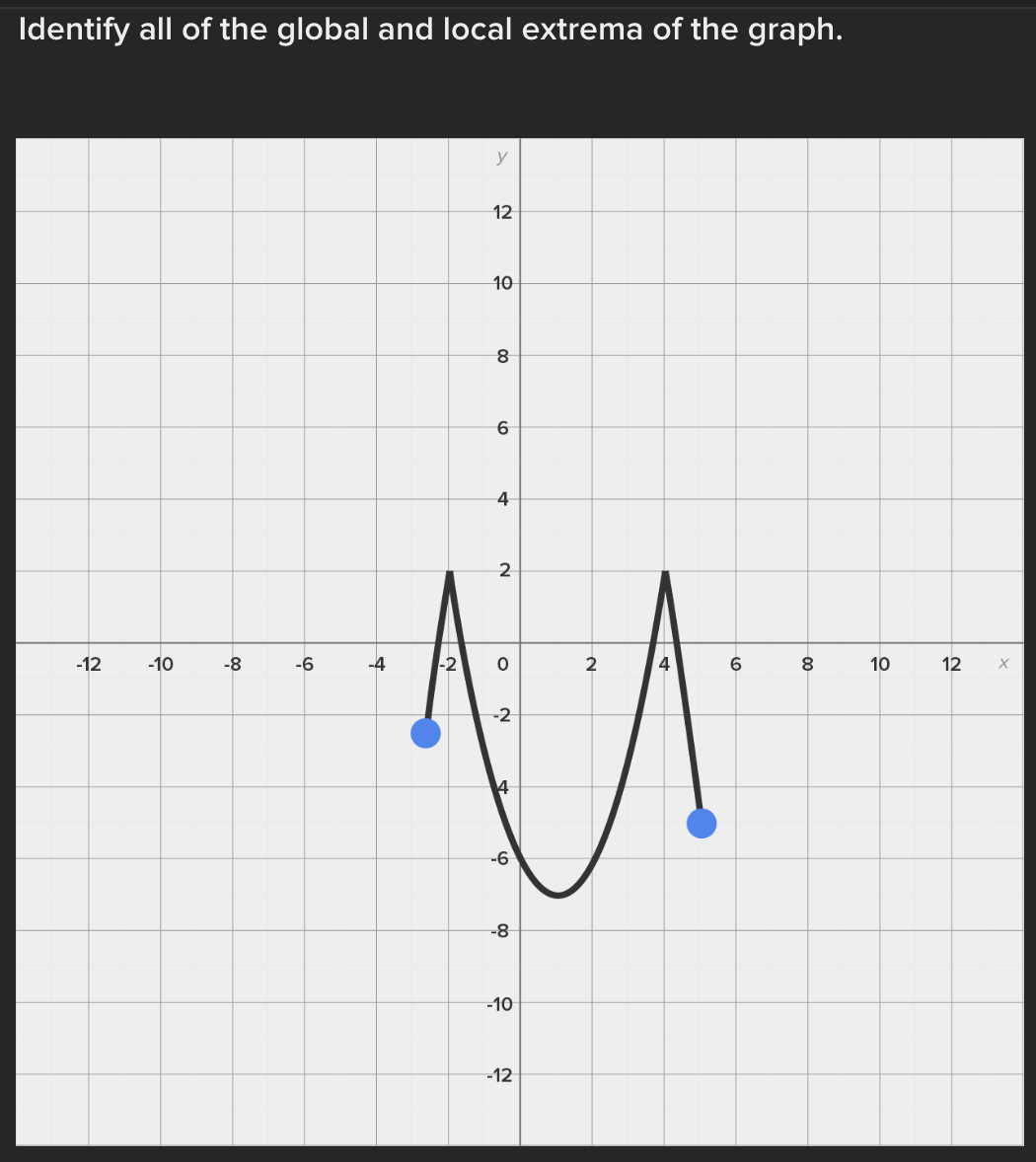
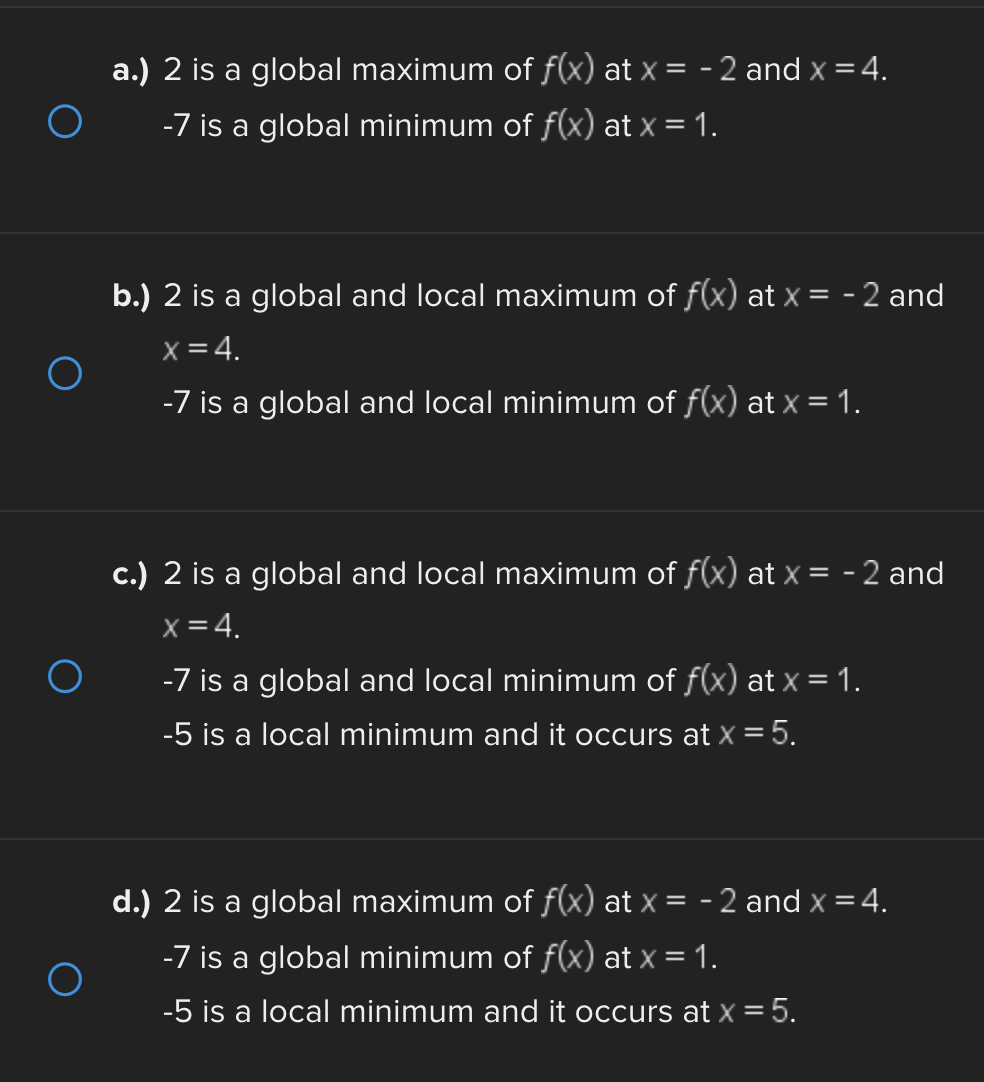


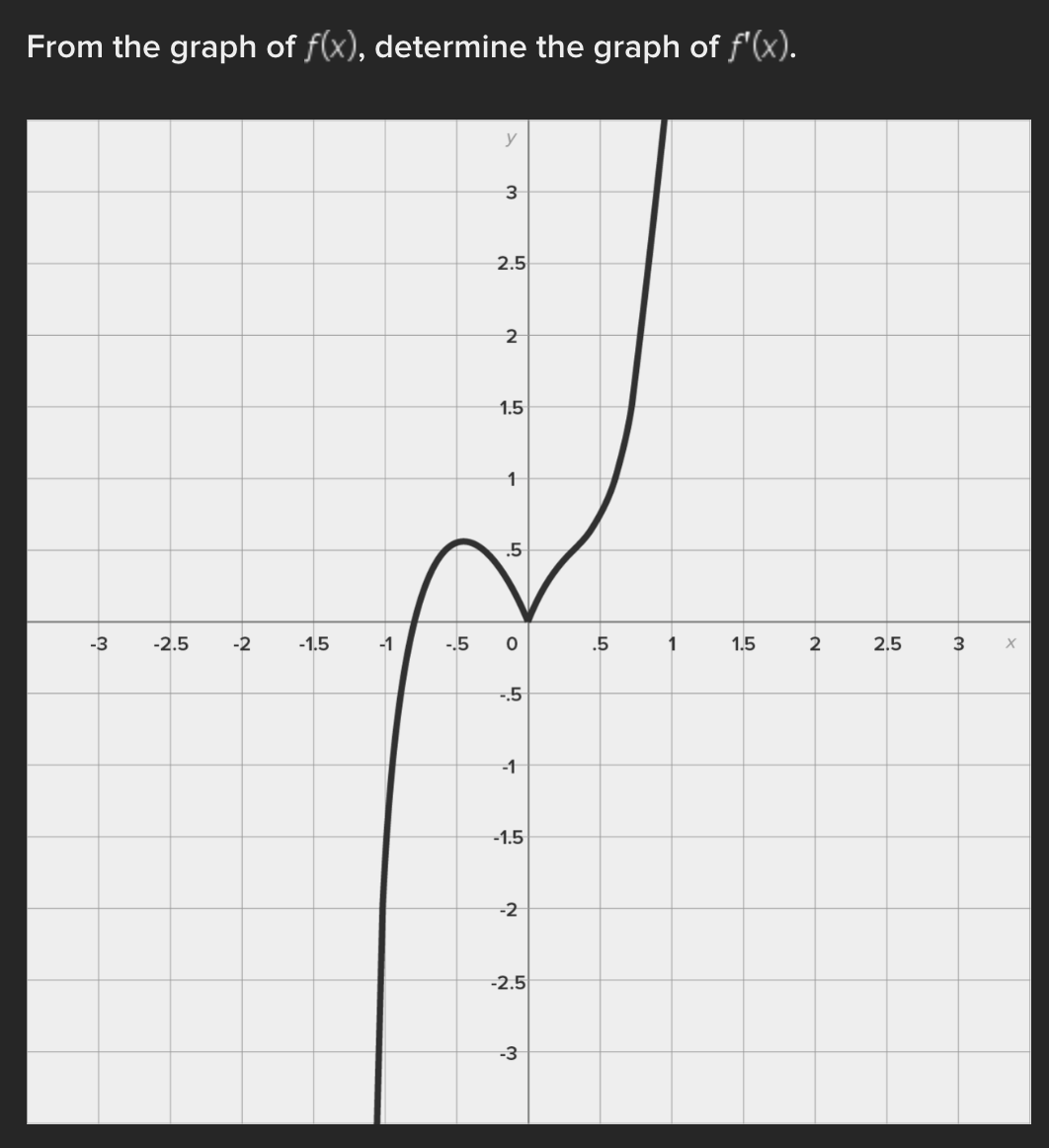
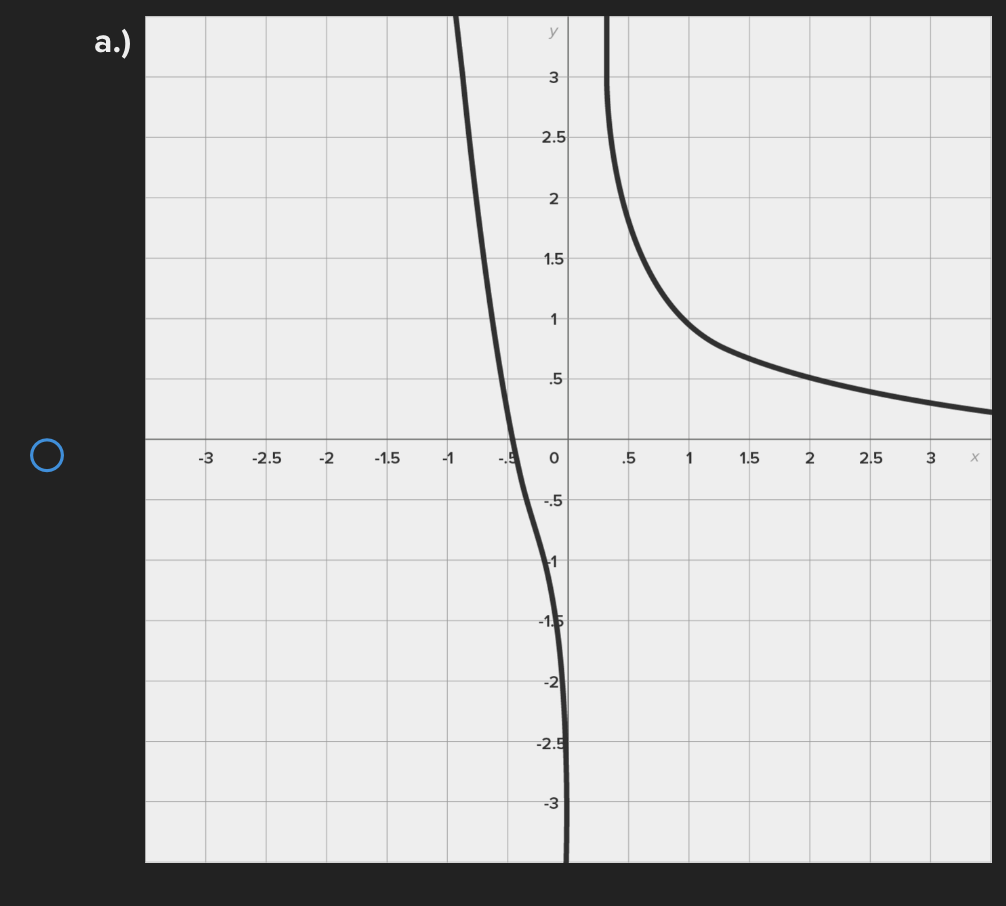
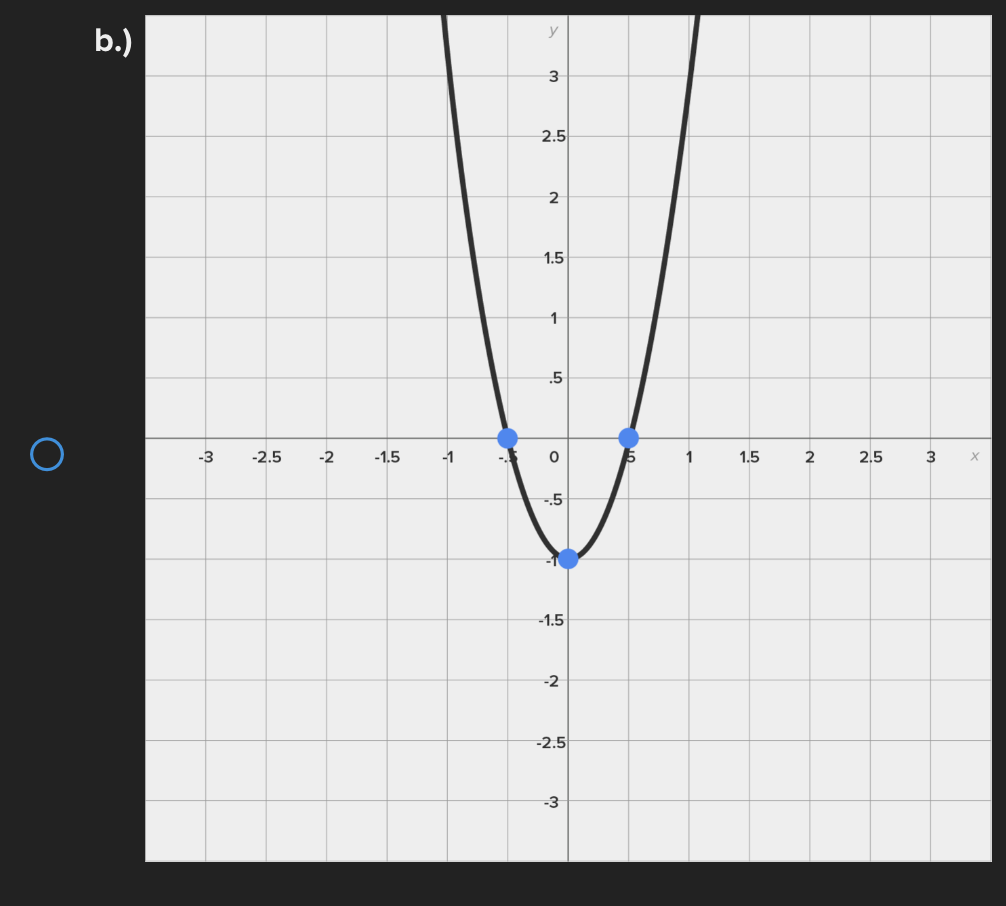


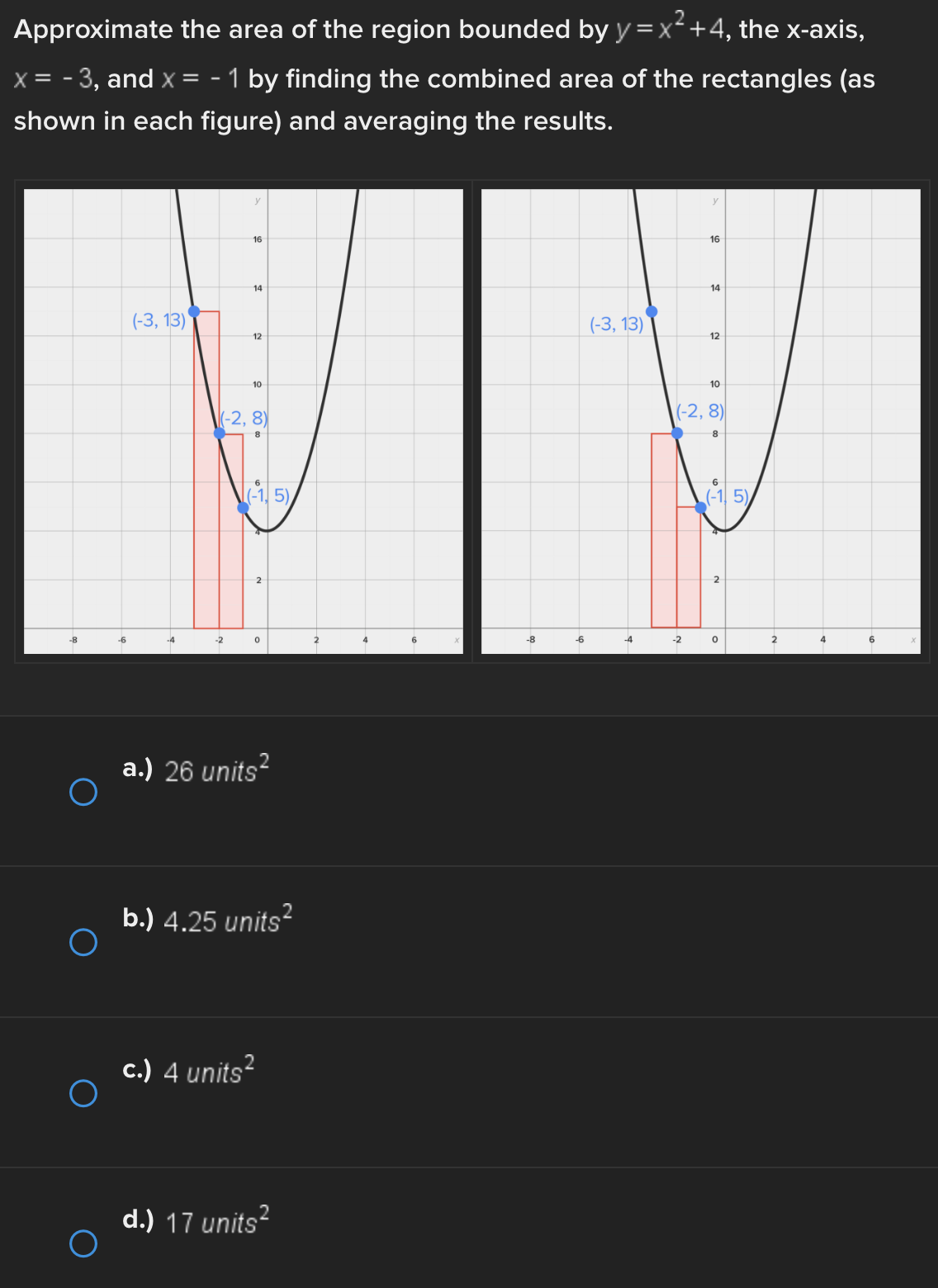
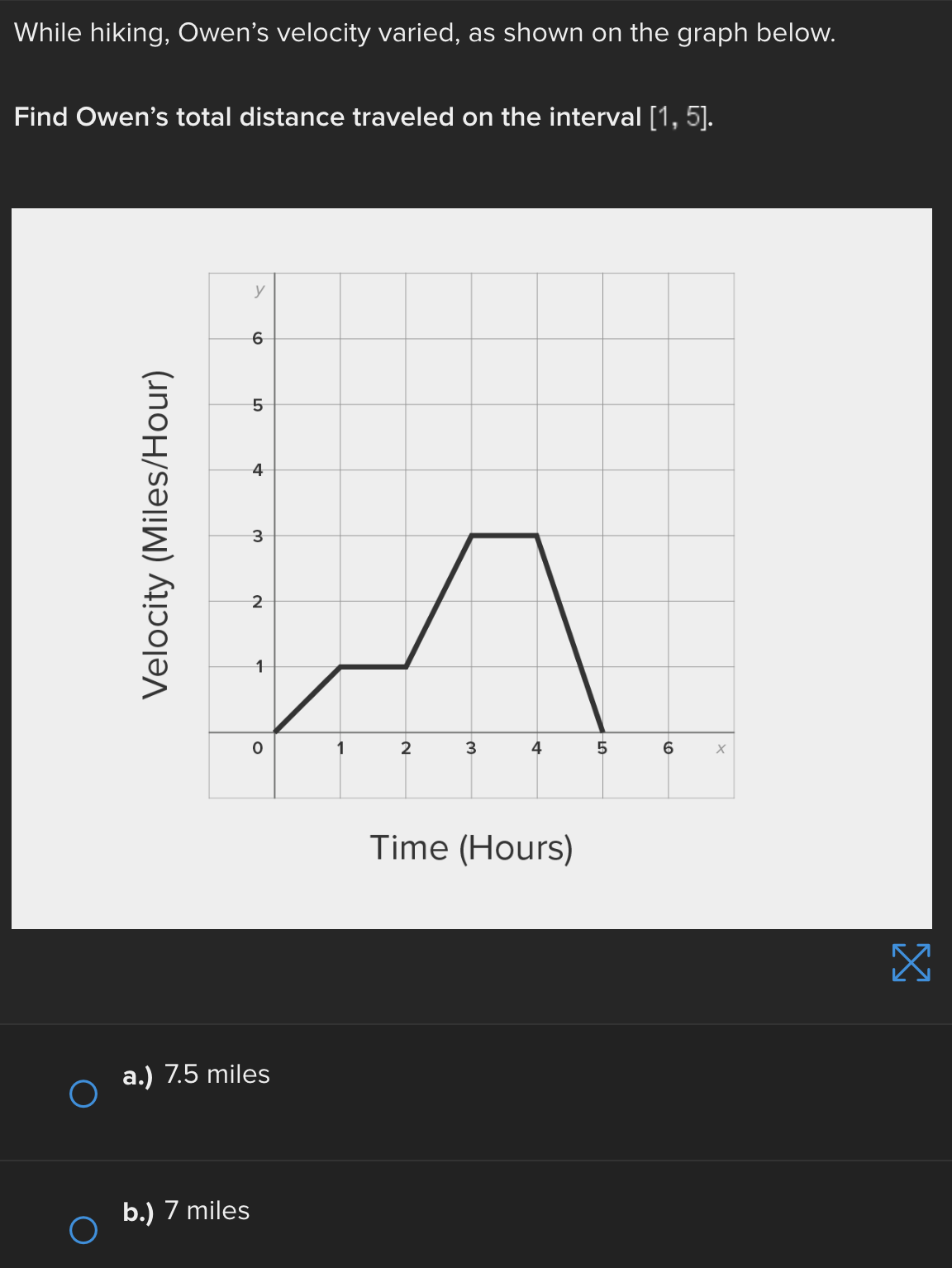
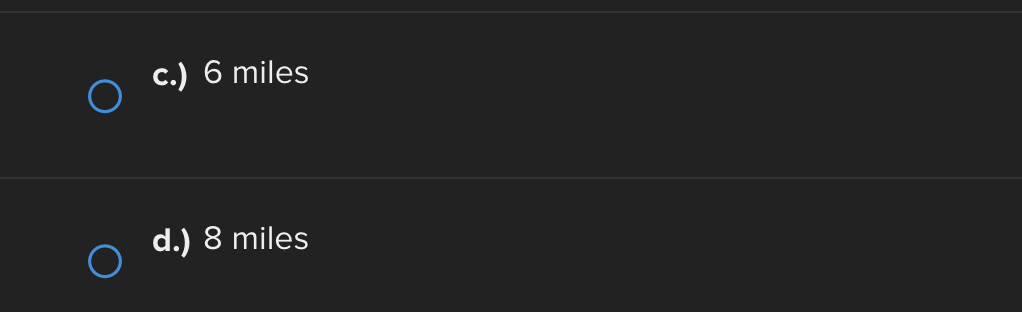
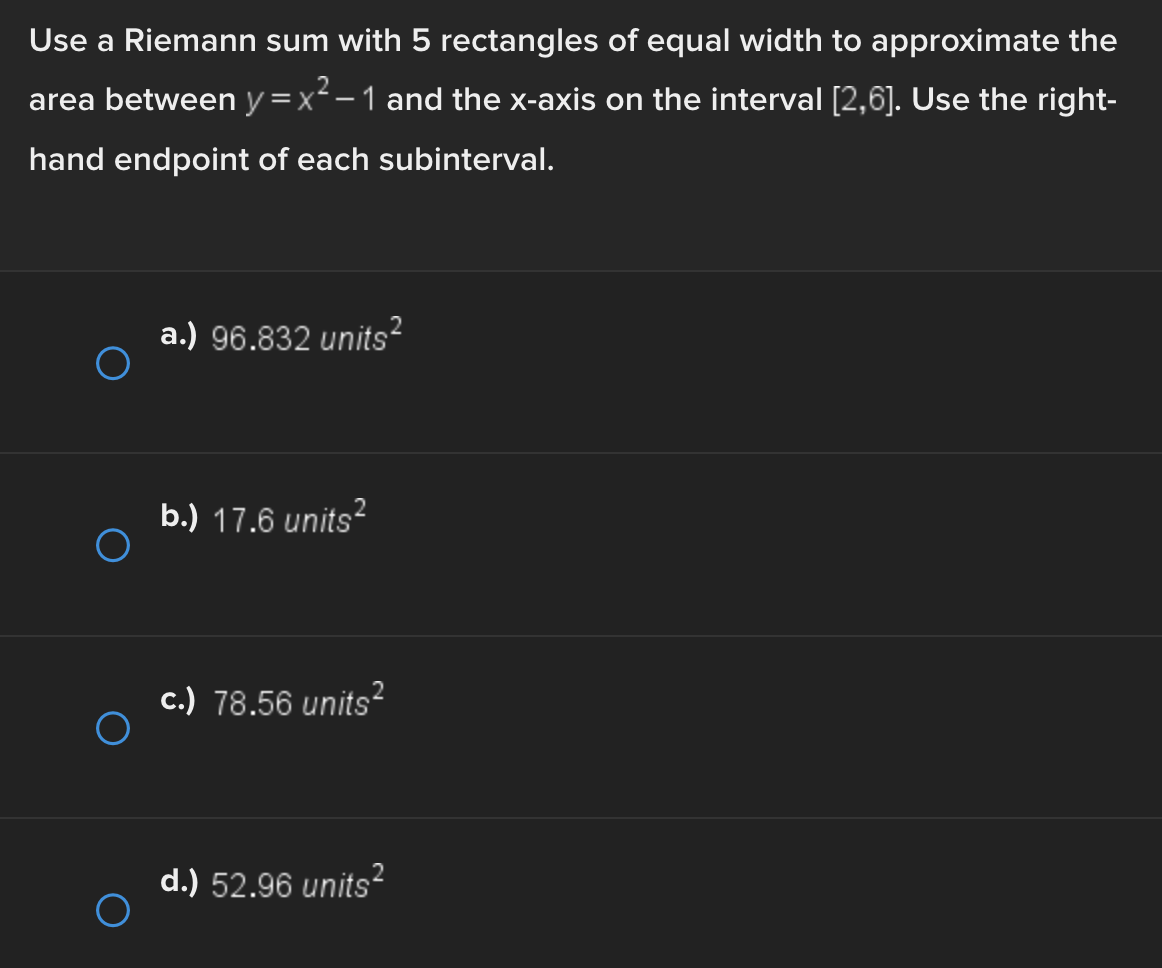
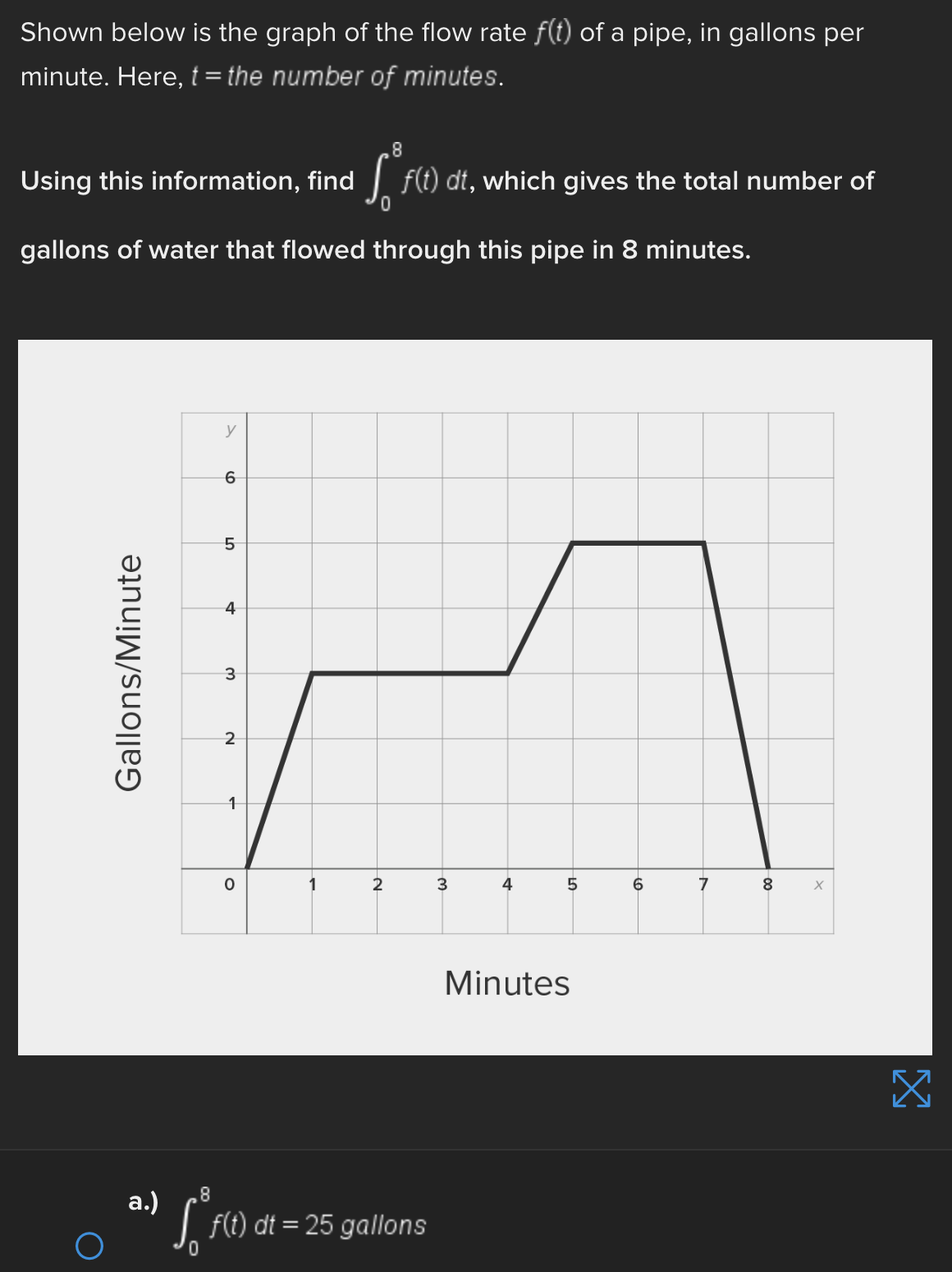

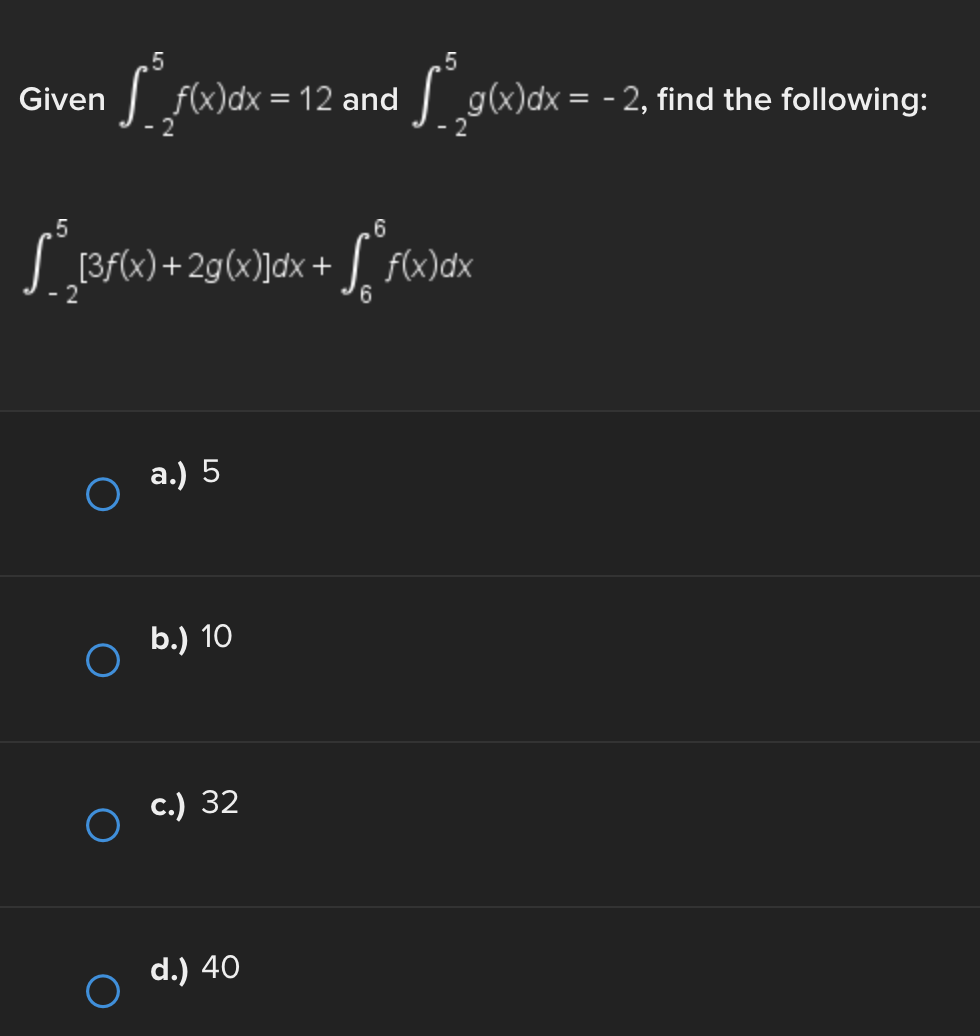
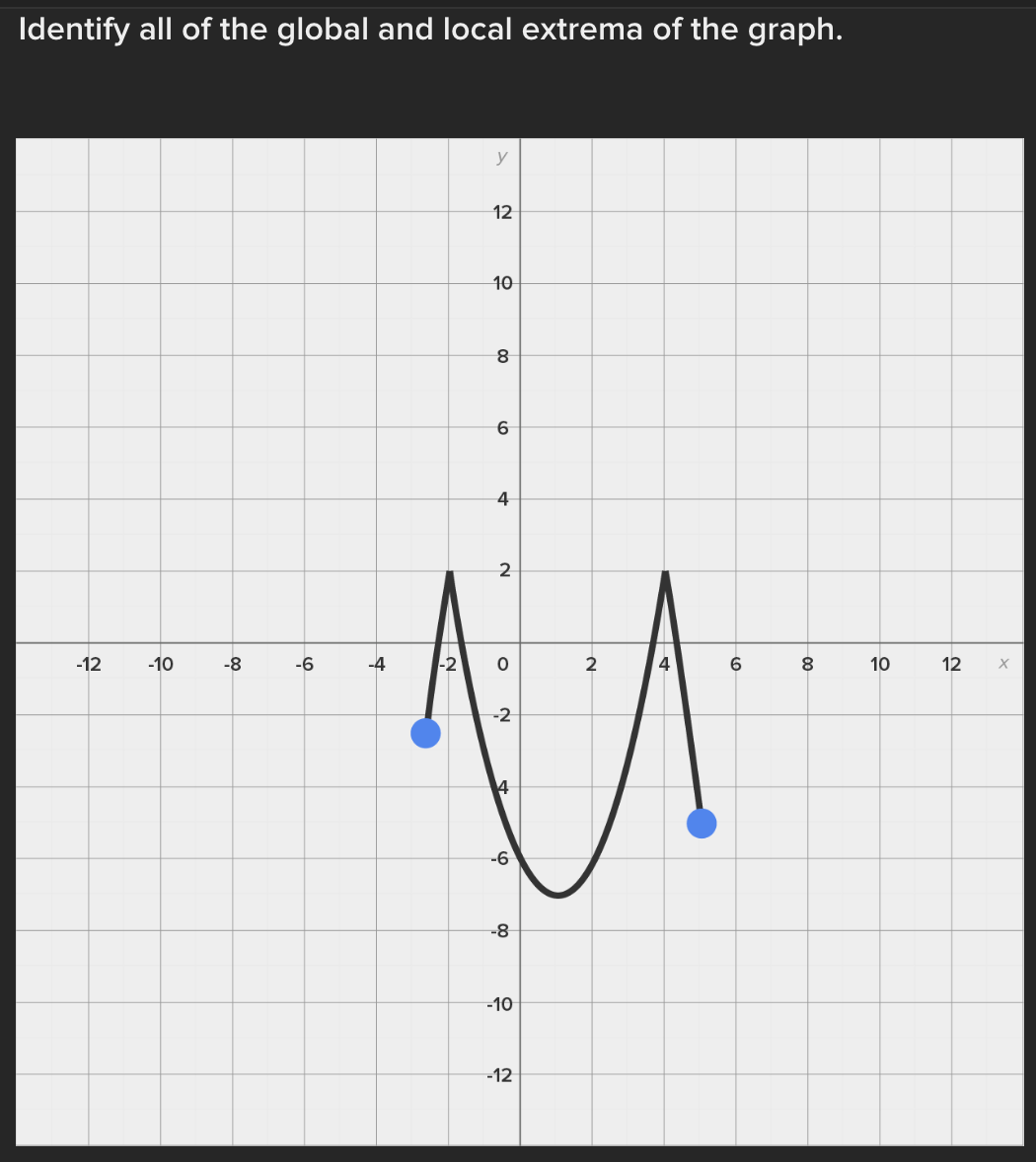
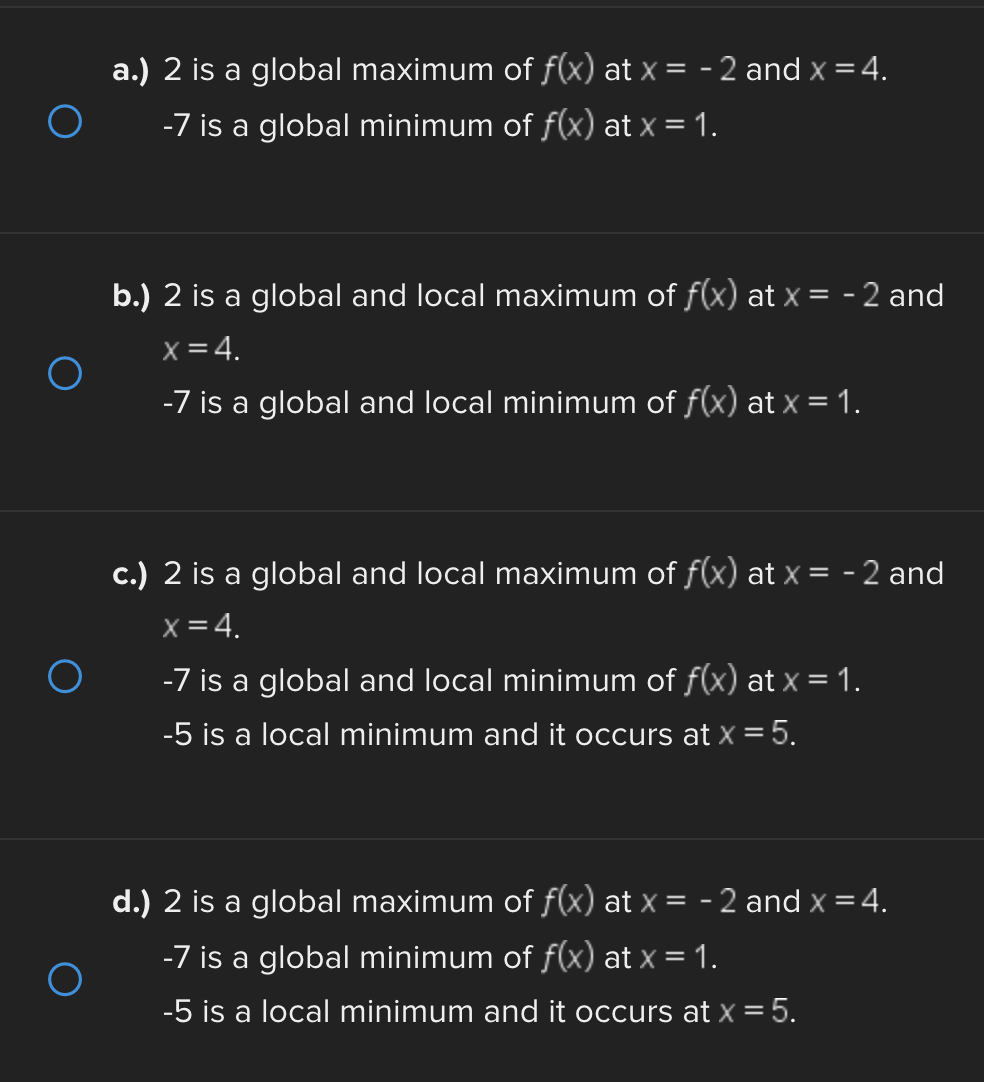
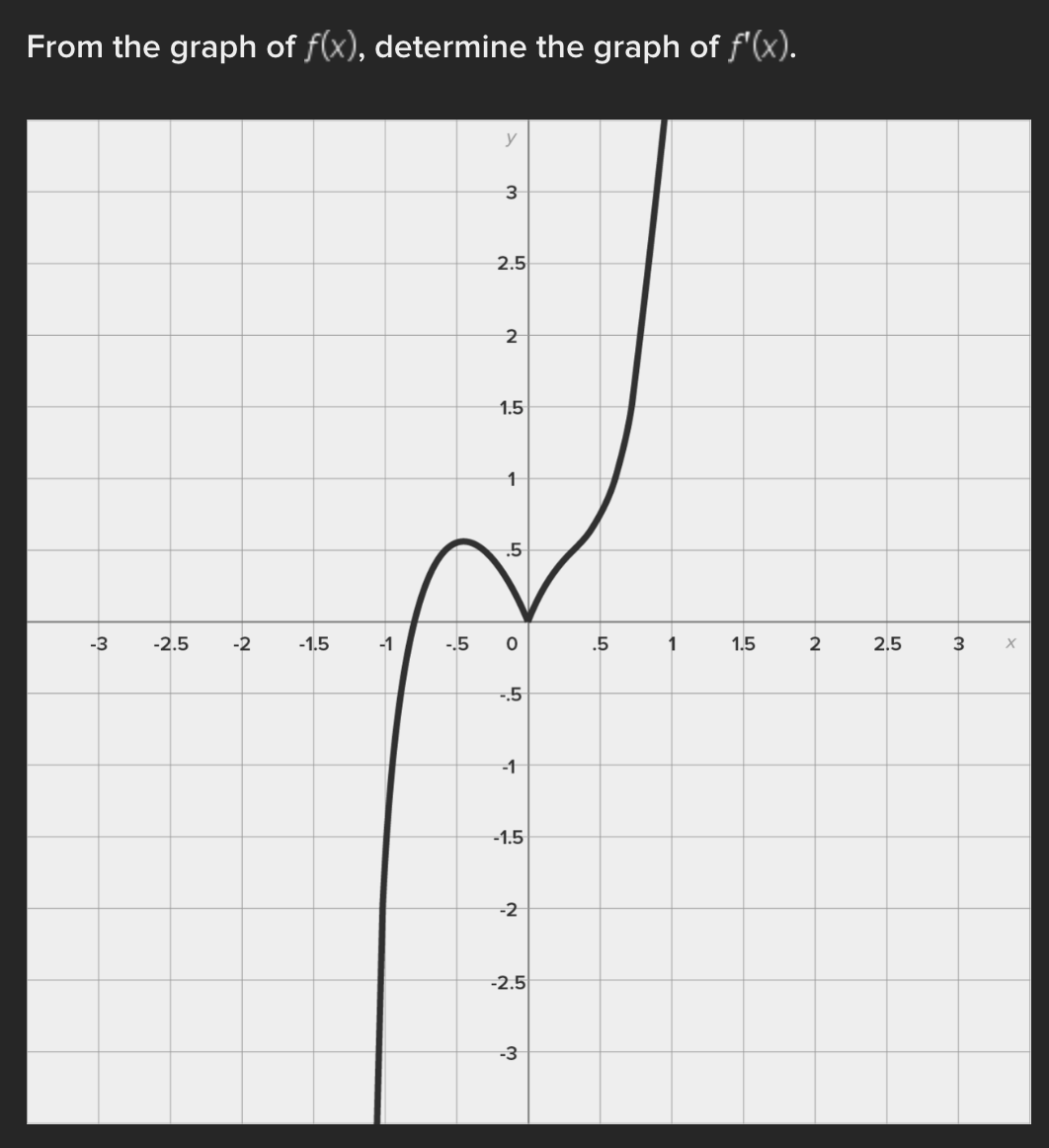
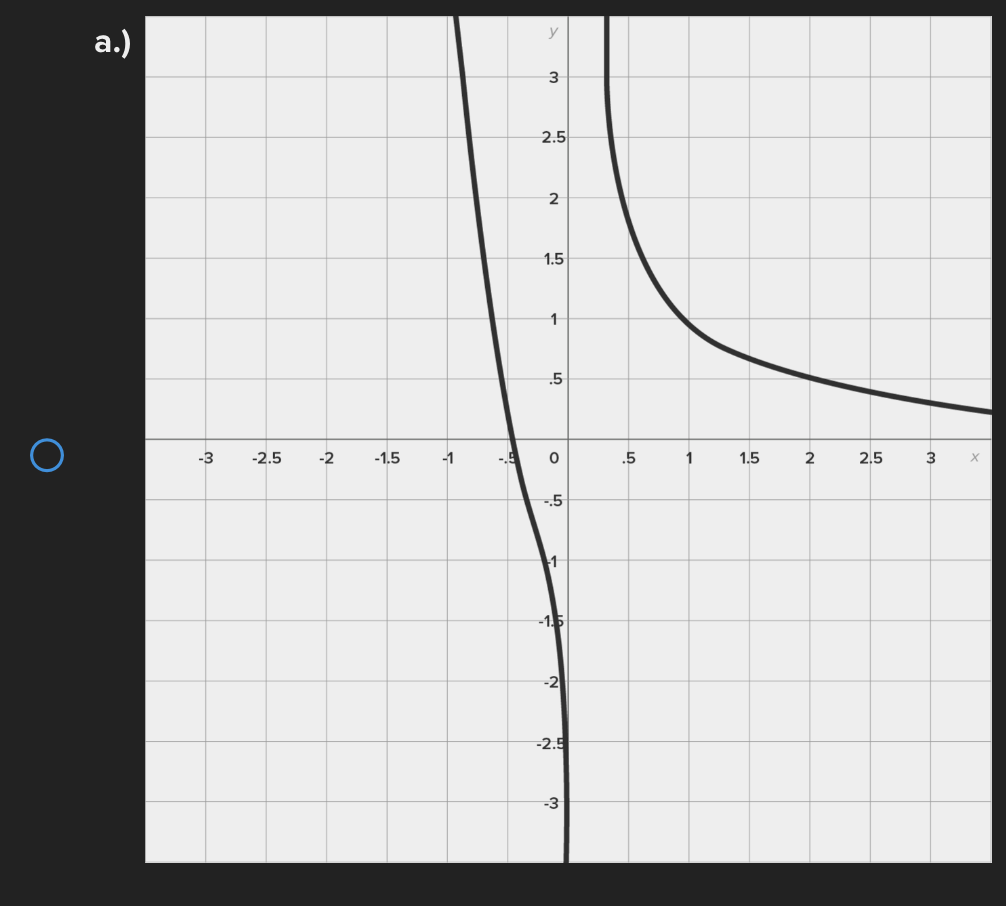
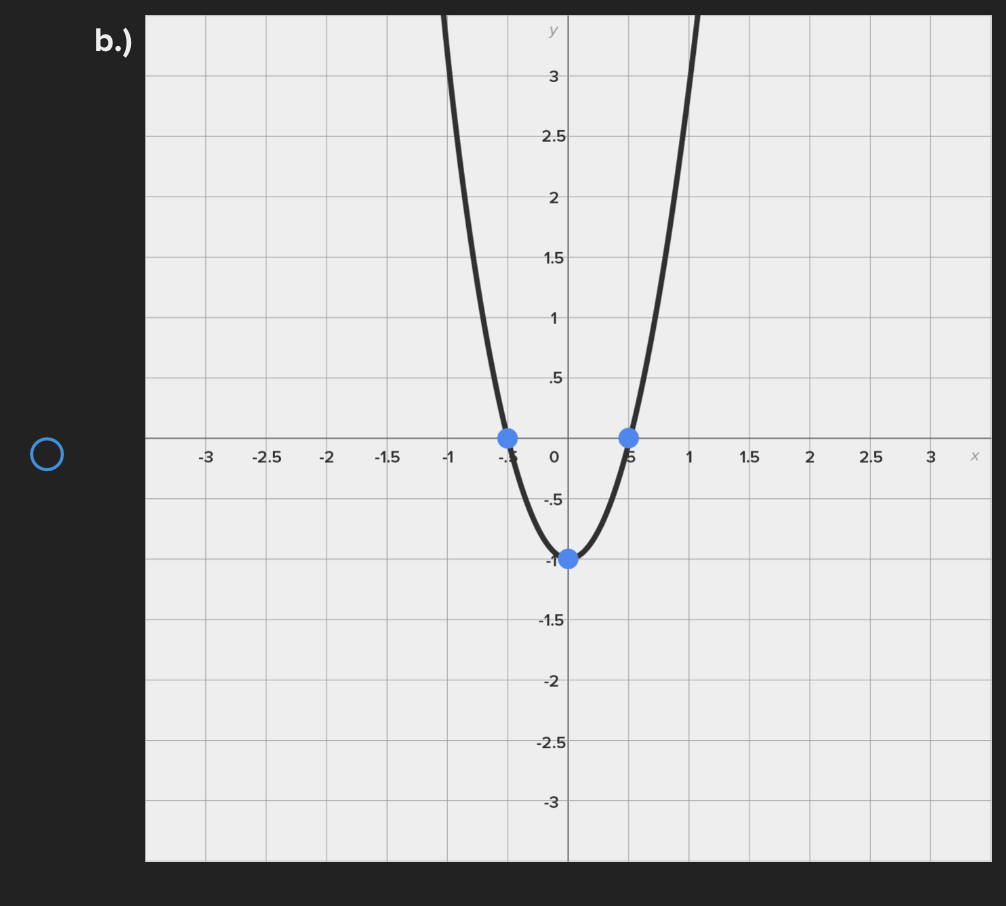
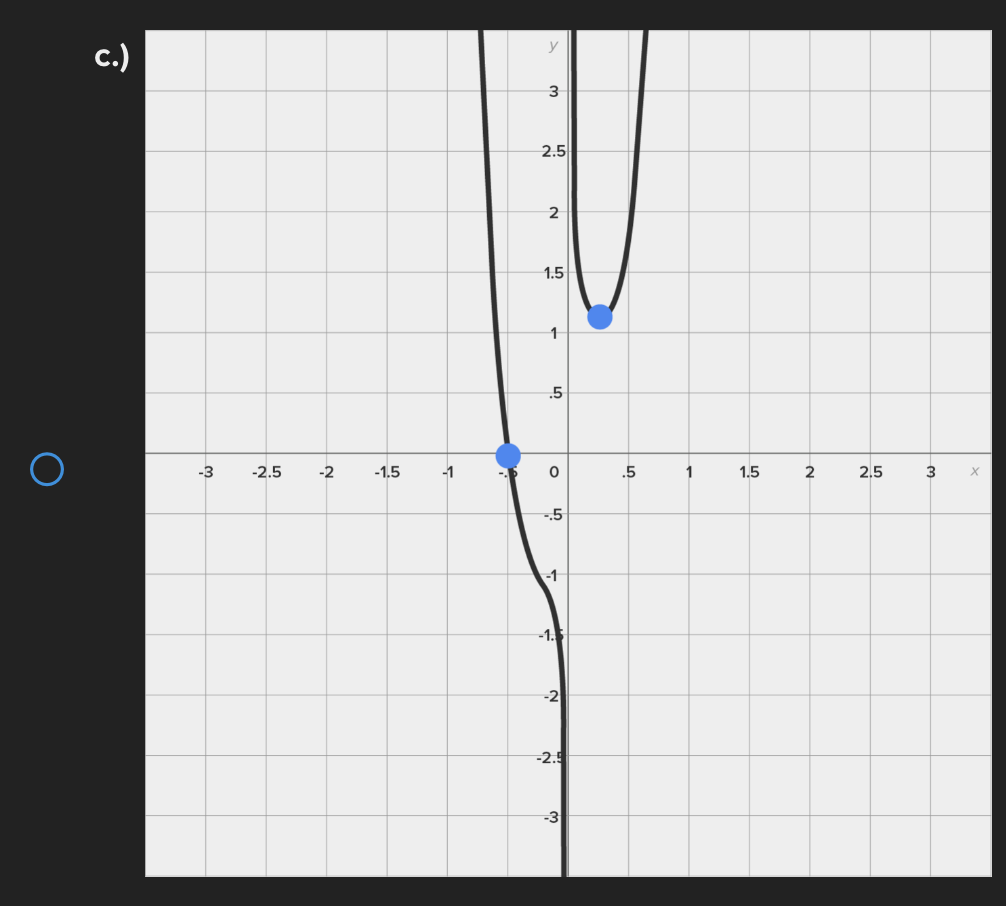
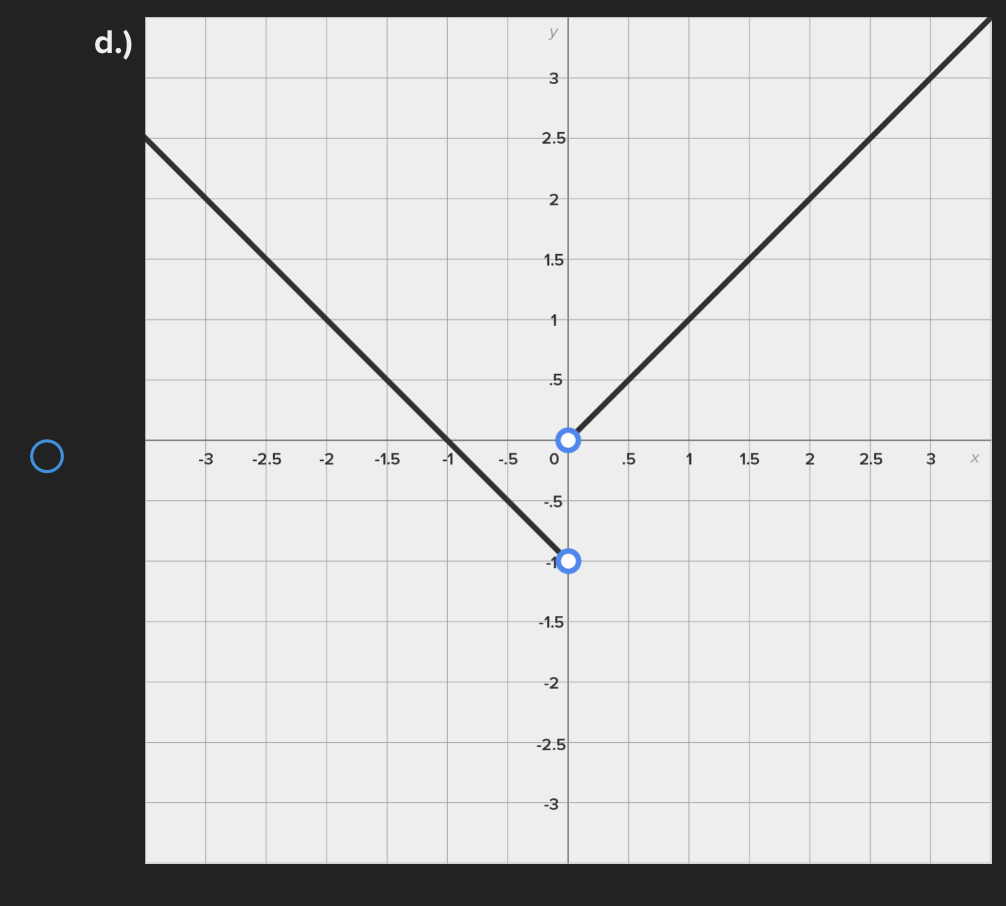
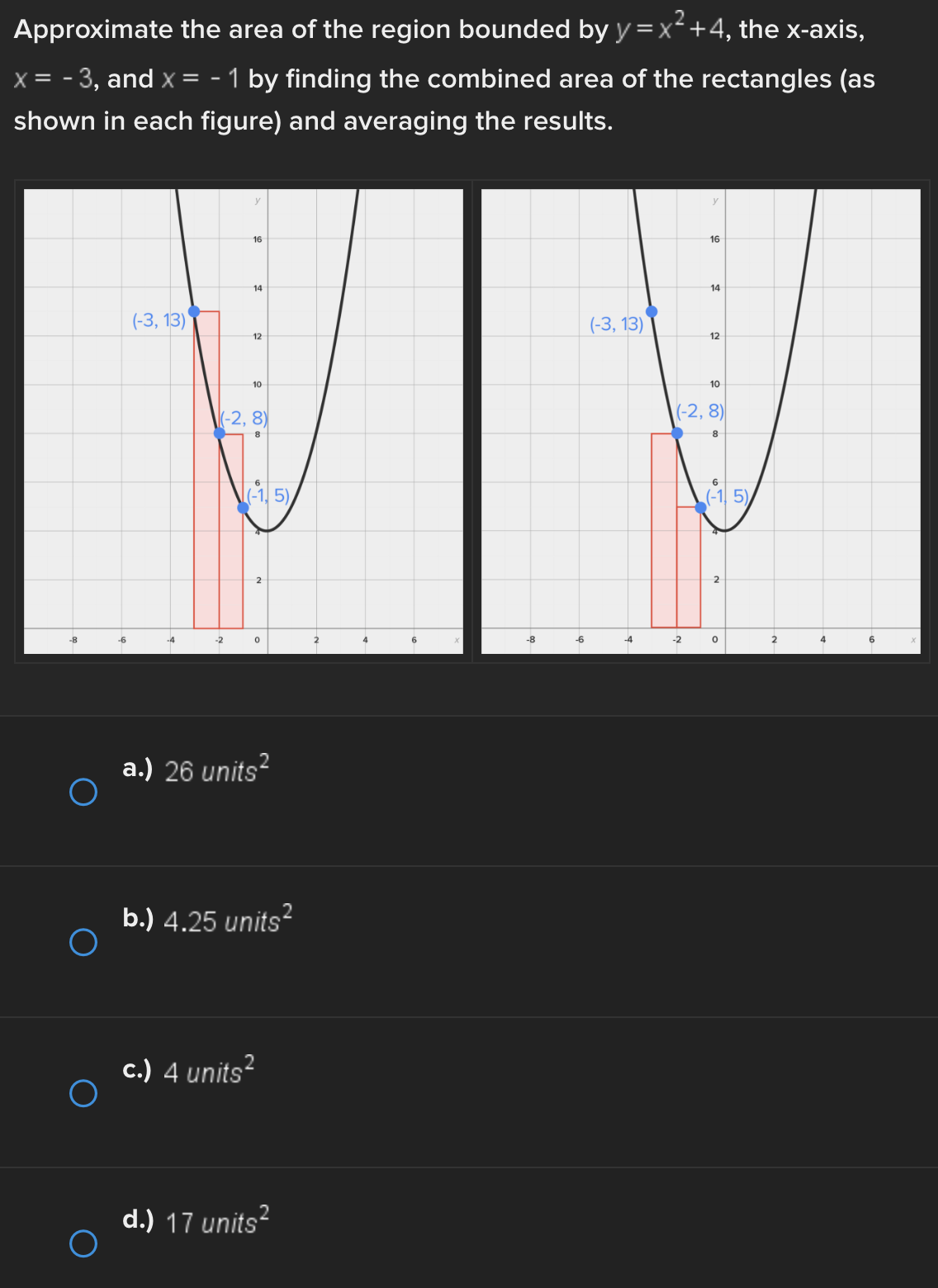
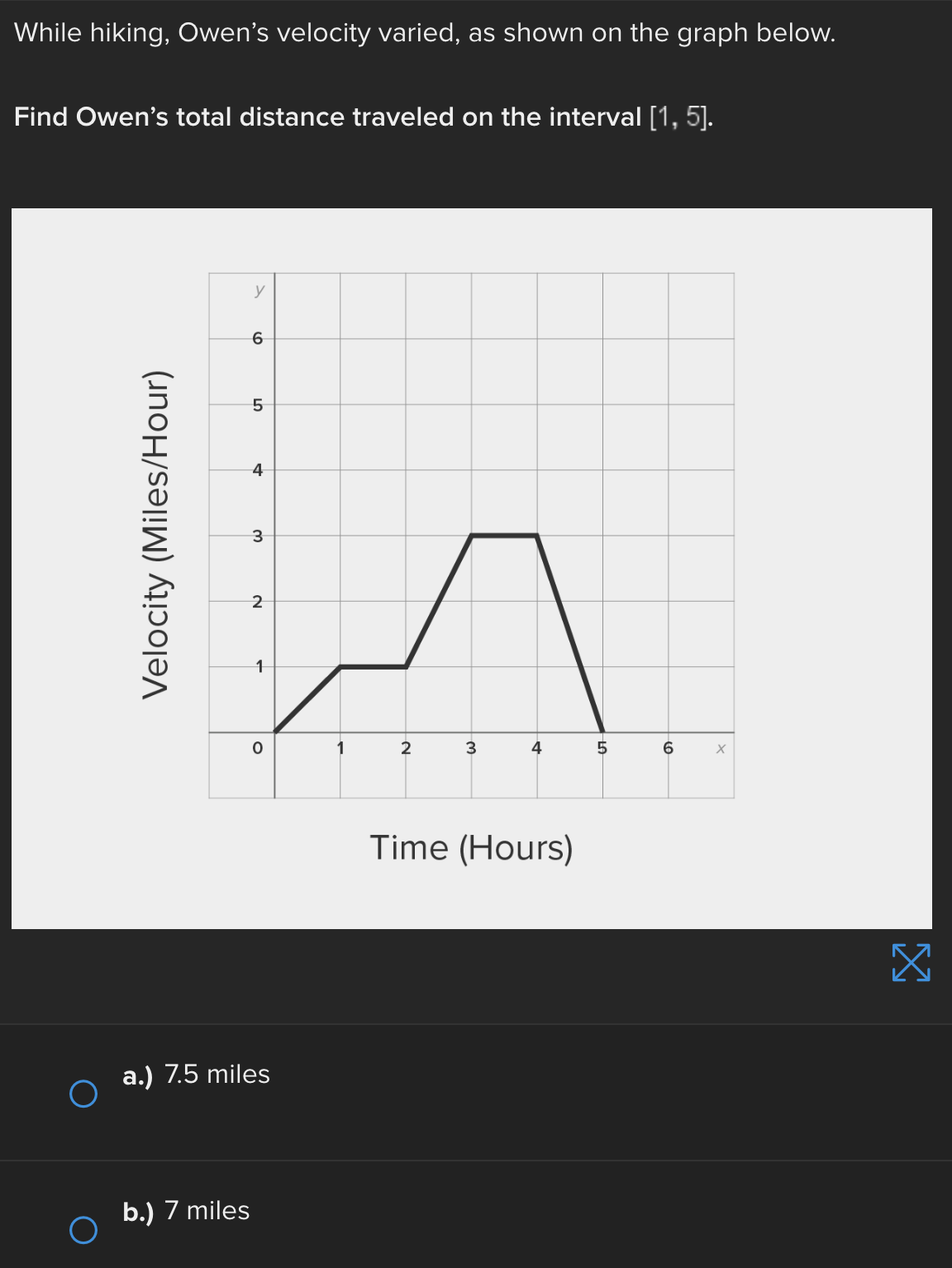
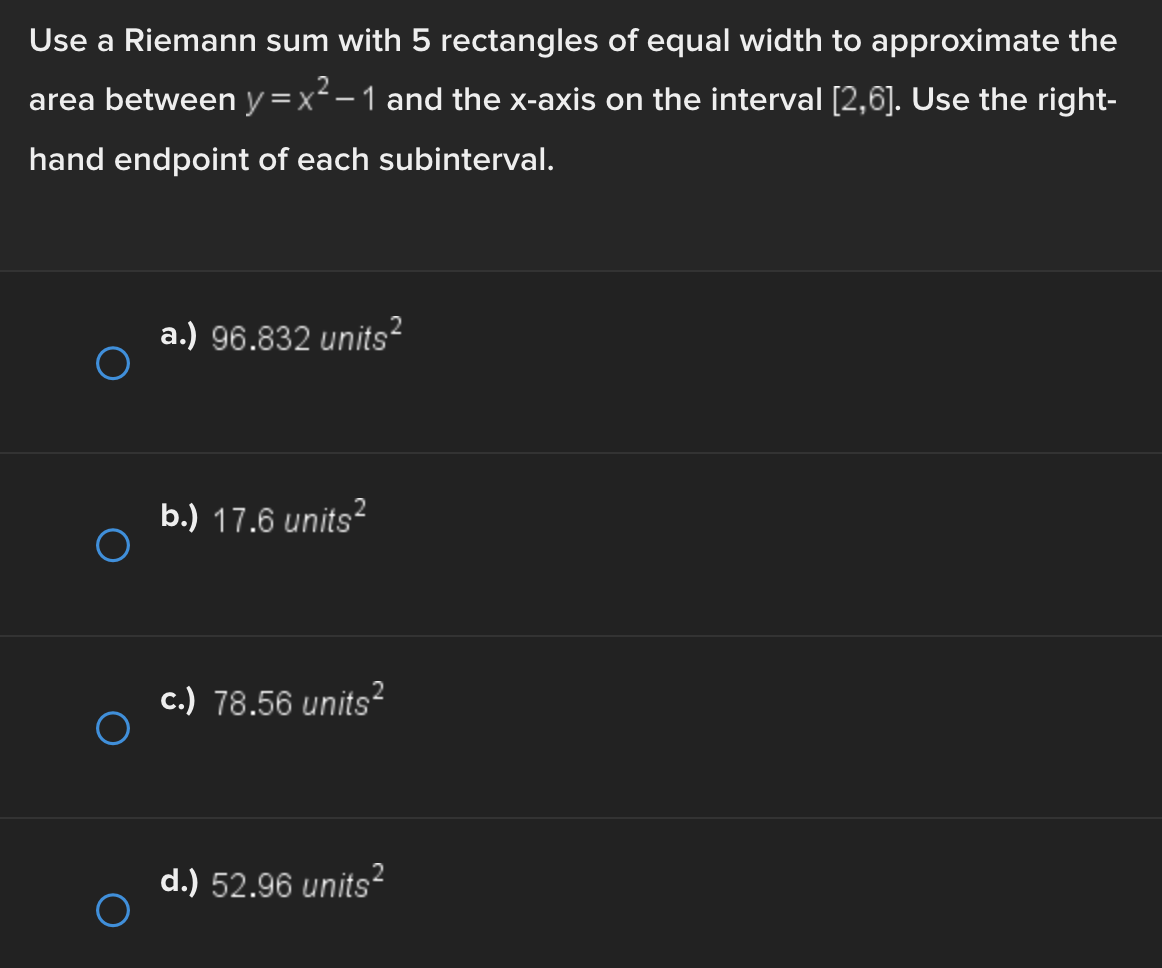
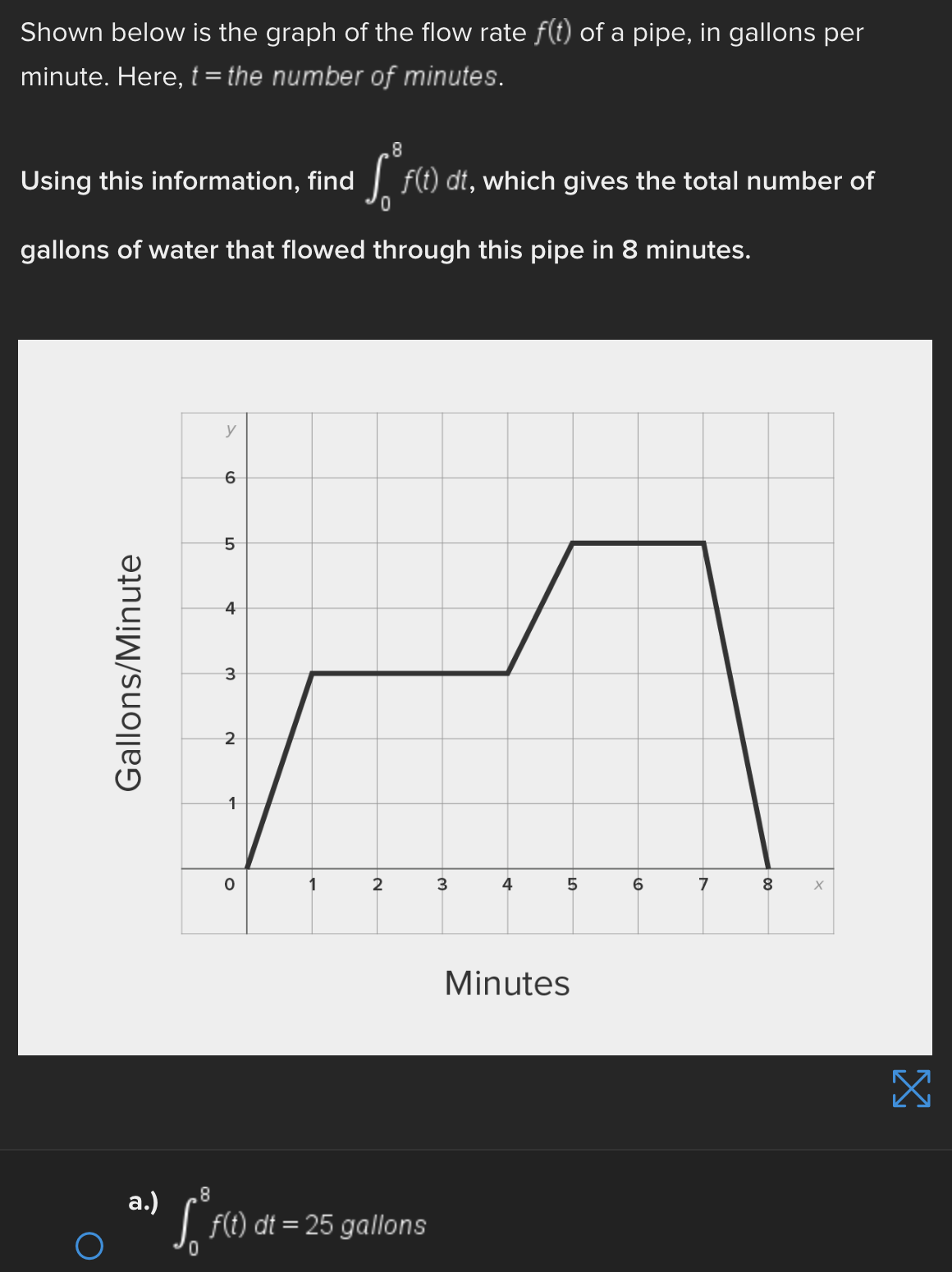
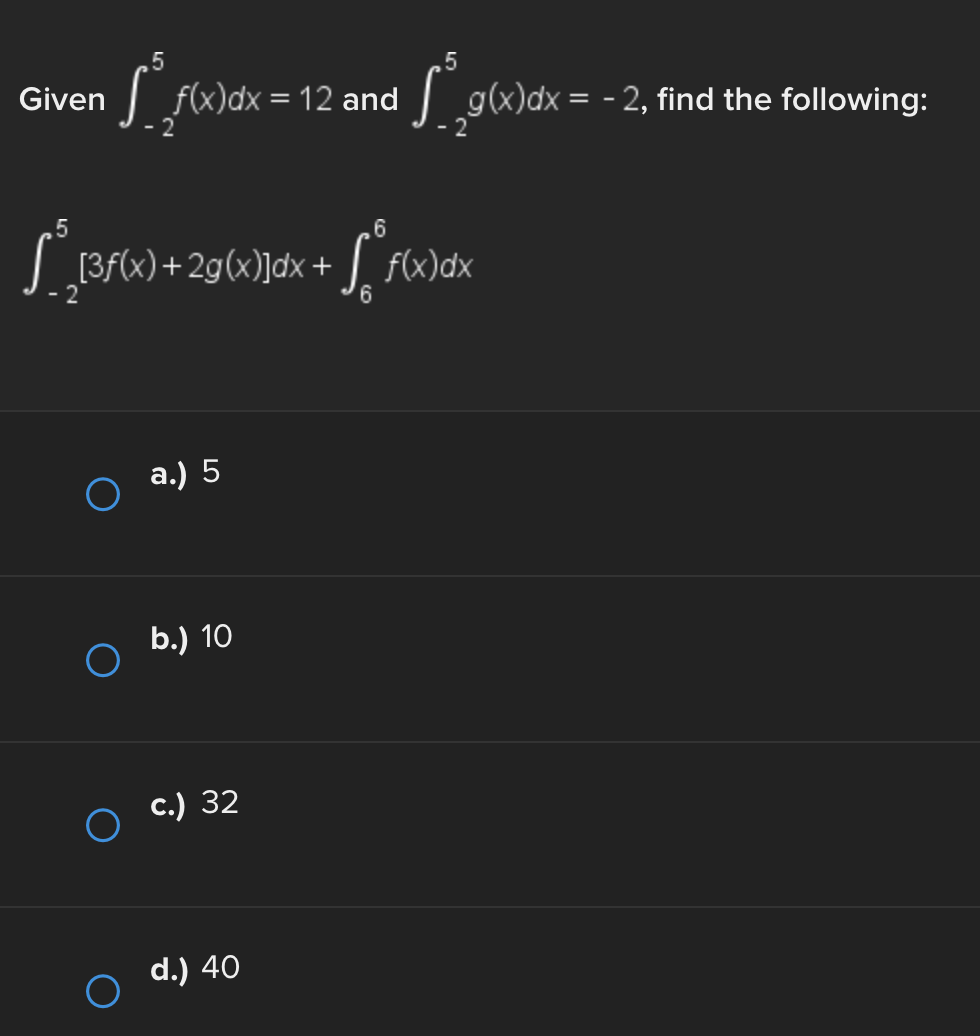
Consider the function f(x) = e* near x = 0. Find the linear approximation error when using the linear approximation to estimate e 0-45 O a.) -0.1183 O b.) 0.1183 ( C.) 1.45 ( d.) -1.45Identify all of the global and local extrema of the graph. a.) 2 is a global maximum of f(x) at x = - 2 and X = 4. O -7 is a global minimum of f(x) at x = 1. b.) 2 is a global and local maximum of f(x) at x = - 2 and X = 4. O -7 is a global and local minimum of f(x) at x = 1. c.) 2 is a global and local maximum of f(x) at x = - 2 and X =4. O -7 is a global and local minimum of f(x) at x = 1. -5 is a local minimum and it occurs at x = 5. d.) 2 is a global maximum of f(x) at x = - 2 and x = 4. O -7 is a global minimum of f(x) at x = 1. -5 is a local minimum and it occurs at x = 5.Determine if the requirements for Rolle's theorem are met by the function f(x) = 5x + on the interval 1 5 . If so, find the values of c in 5. 5 guaranteed by the theorem. a.) f(x) is continuous on any interval not including 0; therefore, it is continuous on 5. 5 . Also, f(x) is not differentiable on (3.5). O Therefore, the conditions of Rolle's theorem have not been met. b.) f(x) is continuous on 51 5 and f(x) is differentiable everywhere except where x = 0, so f(x) is differentiable on O 5 5. When evaluated, f 5 = 26 and f(5) = 26. Therefore, f(a) = f(b) and the conditions of Rolle's theorem are met. The value guaranteed by Rolle's theorem is c = 1.c.) f(x) is continuous on any interval not including 0; therefore, it is continuous on 51 5 . Also, f(x) is differentiable everywhere except where x = 0, so f(x) is O differentiable on 5 5. When evaluated, f 5 = 2 and f(5) = 26. Therefore, f(a) # f(b) and the conditions of Rolle's Theorem are not met. d.) f(x) is continuous and differentiable on any interval not including 0; therefore, it is continuous on 5. 5 and differentiable on 5 5). When evaluated, f = 26 and O f(5) = 26. Therefore, f(a) = f(b) and the conditions of Rolle's theorem are met. The values guaranteed by Rolle's theorem are c = - 1 and c = 1.\fDetermine if the conditions of the mean value theorem are met by the "'I "I function fix) = $ on [-4, 3]. If so, find the values of c in (I -4, 3') .3; guaranteed by the theorem. a.) The function is NOT continuous on [-4, 3], and therefore, the mean value theorem does not apply for this function on the given interval. b.) fix.) is continuous on [-4, 3] and differentiable on the interval (-4.3) The values guaranteed by the mean value theorem are r: = - 6 and .:=0, c.) fix) is continuous on [-4, 3] and differentiable on the interval (-4.3) The values guaranteed by the mean value theorem are .3: -3+V'15. d.) f(x) is continuous on [ - 4, 3] and differentiable on the interval ( - 4, 3). O The values guaranteed by the mean value theorem are C= - 3+V15 .Approximate the area of the region bounded by y = x: +4, the x-axis, x = 3, and x = -1 by finding the combined area of the rectangles (as shown in each figure) and averaging the results. '1 [3-) 4.25 unite" d-) 1? units: While hiking, Owen's velocity varied, as shown on the graph below. Find Owen's total distance traveled on the interval [1, 5]. 5 Velocity (Miles/Hour) 3 2 O 2 3 4 5 6 X Time (Hours) X ( a.) 7.5 miles O b.) 7 miles\fUse a Riemann sum with 5 rectangles of equal width to approximate the area between y = x - 1 and the x-axis on the interval [2,6]. Use the right- hand endpoint of each subinterval. O a.) 96.832 units b.) 17.6 units O O c.) 78.56 units d.) 52.96 units OShown below is the graph of the flow rate f(t) of a pipe, in gallons per minute. Here, t = the number of minutes. 8 Using this information, find / f(t) dt, which gives the total number of gallons of water that flowed through this pipe in 8 minutes. y 6 5 4 Gallons/Minute 3 2 O 2 3 4 5 6 7 8 X Minutes X a.) 8 O f(t) at = 25 gallons 0b.) 8 O f(t) dt = 27 gallons C.) O f(t) at = 29.5 gallons 0 d.) 8 O f(t) dt = 26.5 gallons5 Given 2 f(x)dx = 12 and g(x)dx = - 2, find the following: 5 6 [3f(x)+2g(x)]dx + | f(x)dx O a.) 5 O b.) 10 O C.) 32 O d.) 40
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


