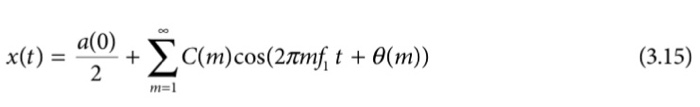
3.5 Construct the sawtooth wave shown below and use the MATLAB fft routine to find the frequency spectrum of this waveform. Then reconstruct the square wave using the first 24 components using Equation 3.15. Do not plot the spectrum, but plot the original and reconstructed waveform superimposed. Make 1024 and N = 1024 to represent the 1-s periodic waveform. [Hint: The MATLAB fft routine does no scaling; so, you will have to scale the output to get the correct reconstructed waveform. Also, remember that the first element of the complex vector produced by the fft routine is the DC component (that will be 0.0 for this waveform) and the first complex sinusoidal coefficient is in the second element.] (0 (3.15) m-l 3.5 Construct the sawtooth wave shown below and use the MATLAB fft routine to find the frequency spectrum of this waveform. Then reconstruct the square wave using the first 24 components using Equation 3.15. Do not plot the spectrum, but plot the original and reconstructed waveform superimposed. Make 1024 and N = 1024 to represent the 1-s periodic waveform. [Hint: The MATLAB fft routine does no scaling; so, you will have to scale the output to get the correct reconstructed waveform. Also, remember that the first element of the complex vector produced by the fft routine is the DC component (that will be 0.0 for this waveform) and the first complex sinusoidal coefficient is in the second element.] (0 (3.15) m-l