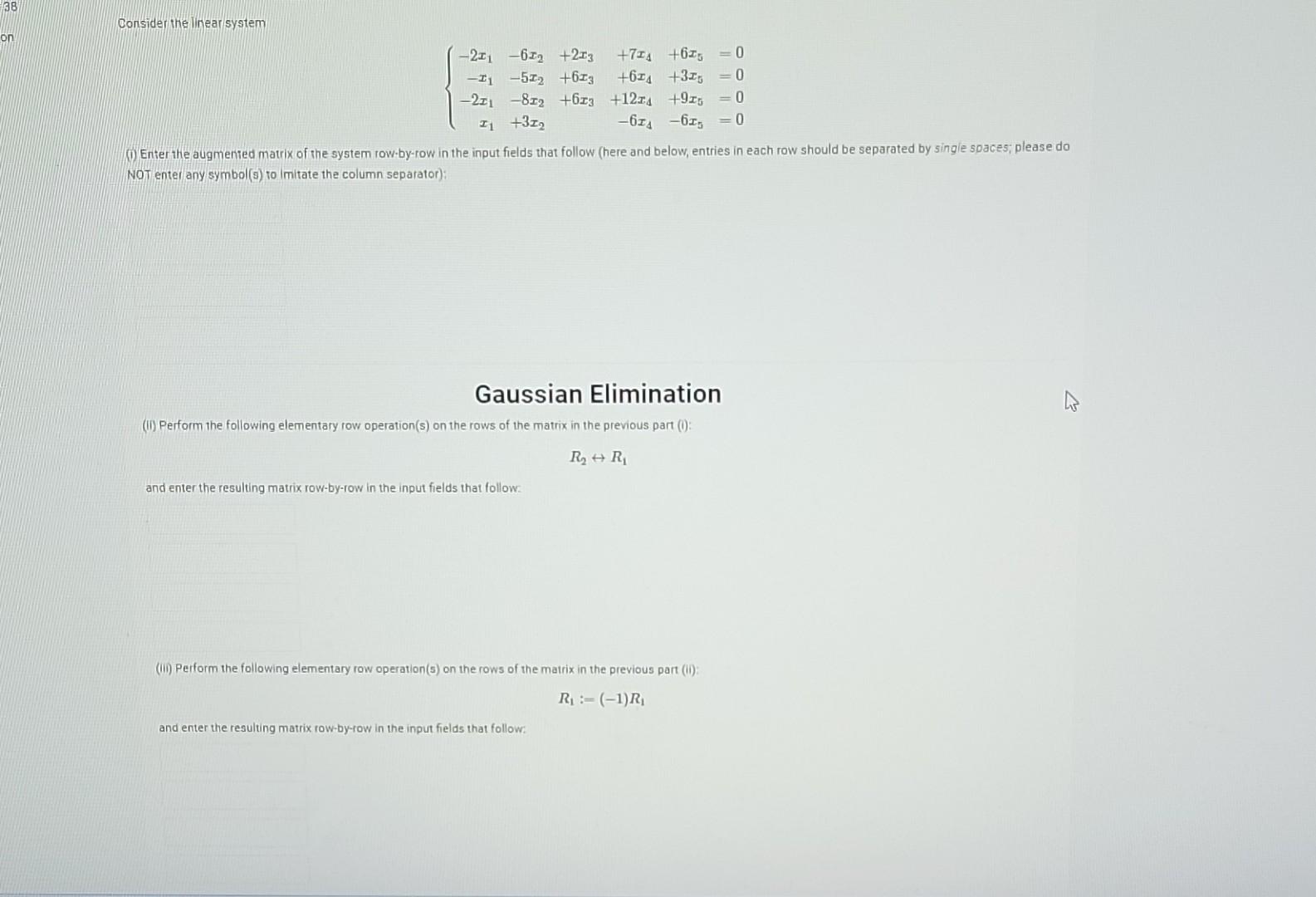
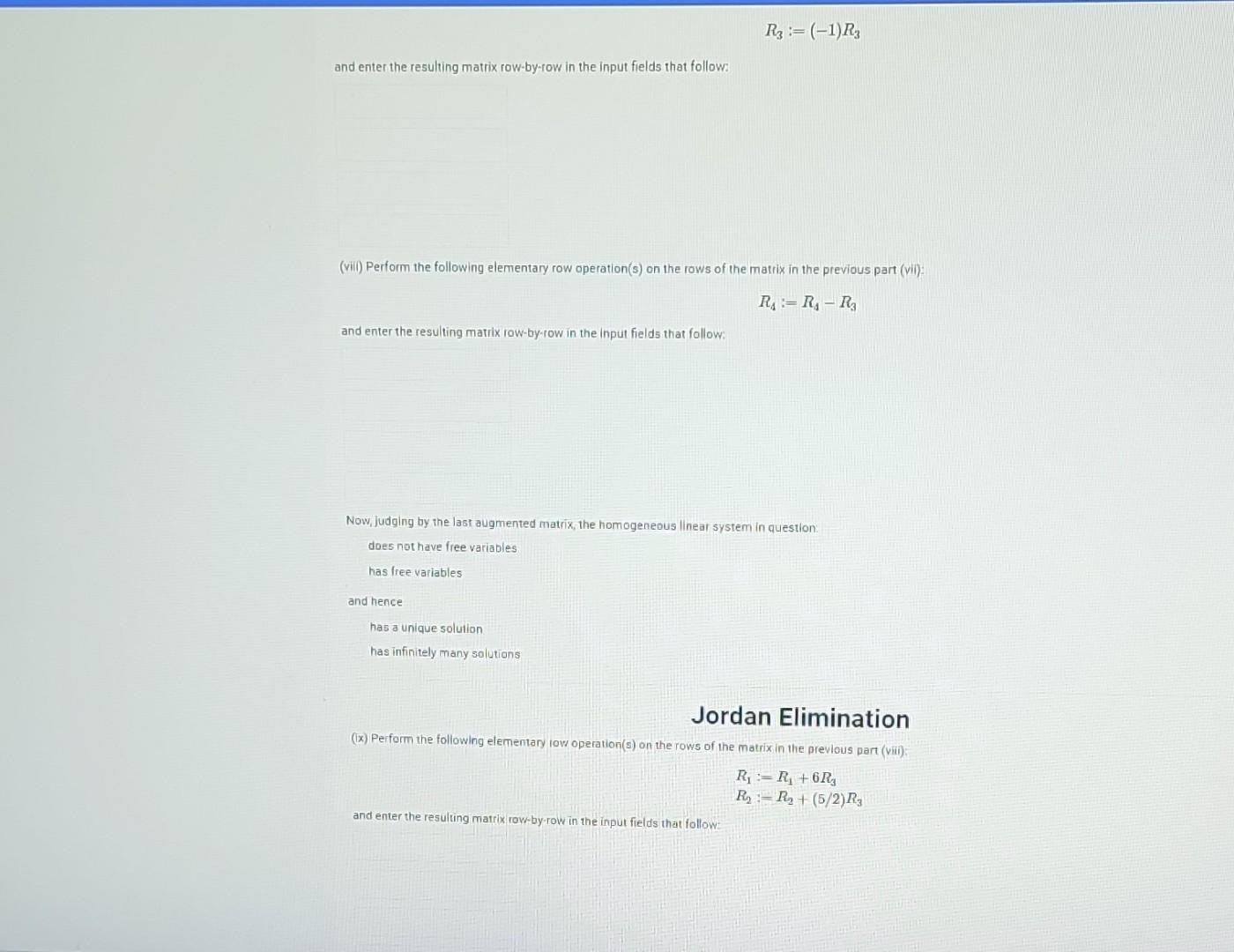
38 on Consider the linear system -22-61 +213 -11-57 +623 -211 -812 +673 71 +37 (0) Enter the augmented matrix of the system row-by-row in the input fields that follow (here and below, entries in each row should be separated by single spaces; please do NOT enter any symbol(s) to imitate the column separator): +71 +61 = 0 +6 +31 = 0 +1274 +975 = 0 -61-62 = 0 Gaussian Elimination (II) Perform the following elementary row operation(s) on the rows of the matrix in the previous part (1): R + R and enter the resulting matrix row-by-row in the input fields that follow: (1) Perform the following elementary row operation (s) on the rows of the matrix in the previous part (ii): R:- (-1) R and enter the resulting matrix row-by-row in the input fields that follow: (iv) Perform the following elementary row operation (s) on the rows of the matrix in the previous part(): R R+2R R3 R3+2R R = R R and enter the resulting matrix fow-by-row in the input fields that follow: (v) Perform the following elementary row operation(s) on the r of the and enter the resulting matrix row-by-row in the input fields that follow: the previous part (iv): R = (1/4) R (vi) Perform the following elementary row operation (s) on the rows of the matrix in the previous part (V): R: R-2R RR+2R and enter the resulting matrix row-by-row in the input fields that follow: (vii) Perform the following elementary row operation(s) on the rows of the matrix in the previous part (vi): R3:- (-1) R and enter the resulting matrix row-by-row in the input fields that follow: (vii) Perform the following elementary row operation(s) on the rows of the matrix in the previous part (vii): R = R R and enter the resulting matrix row-by-row in the input fields that follow: Now, judging by the last augmented matrix, the homogeneous linear system in question. does not have free variables. has free variables and hence R3=(-1) R has a unique solution has infinitely many solutions Jordan Elimination (ix) Perform the following elementary row operation(s) on the rows of the matrix in the previous part (viii): RR +6R R-R+ (5/2) R3 and enter the resulting matrix row-by-row in the input fields that follow: (x) Perform the following elementary row operation(s) on the rows of the matrix in the previous part (ix): R-R-5R and enter the resulting matrix row-by-row in the input fields that follow: Analyze the last augmented matrix to see that it is indeed in reduced row echelon form. General Solution (xi) Use (x) to obtain the general solution of the system, and enter it in the input fields below (If any of the equations is not necessary, please enter an asterisk in both input fields reserved for the equation): Fundamental Set of Solutions (xil) Finally, use (xi) to obtain the standard fundamental set of solutions (FSS) of the homogenous linear system in question, and then enter the coordinates of the vectors in the FSS similarly to of to 1,1,-2/1 0,1) (1, 1, -2/5, 0, 1 T If a particular vector is not necessary, please enter an asterisk in the input field reserved for it. If the system has no fundamental set of solutions (due to the absence of free variables), enter an asterisk in each input field. 3 ( (T