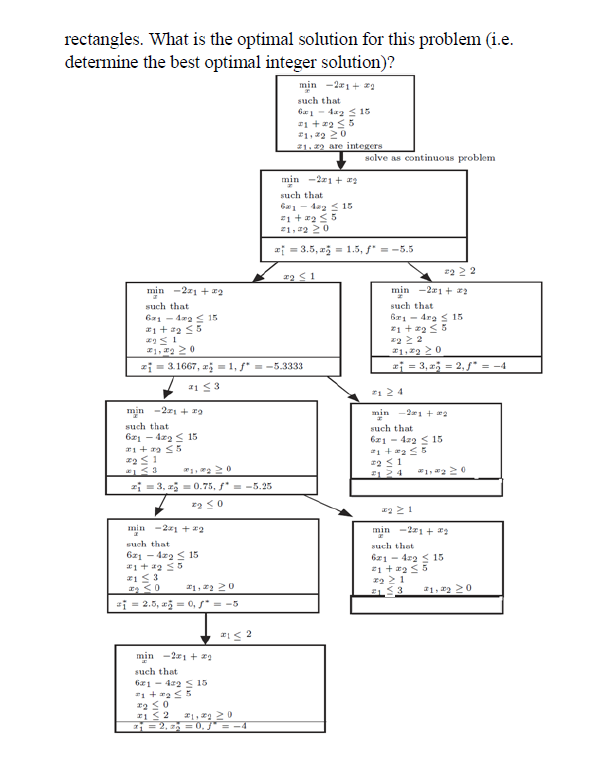
3)The following linear discrete optimization problem is solved using the branch and bound method. min -2x1 + x2 Subject to 6x1 - 4x2 15 x1+x25 x1, x20 x1, x2 Z The solution procedure is represented as in the following flow diagram. First: By using linprog function in MATLAB (If necessary), determine the solution for the branches with blank rectangles. What is the optimal solution for this problem (i.e. determine the best optimal integer solution)? min -2x1 + x2 such that 61-42 15 1+2 5 1,22 20 21.29 are integers min -2x1+x2 solve as continuous problem such that #1+2 5 #1, #2 20 x=3.5, 1.5, * = -5.5 2 1 min -221 +22 I such that 631-4915 1+2 5 1,20 3.1667, 1, -5.3333 13 min -221 +9 such that 6x14x215 21+39 5 221