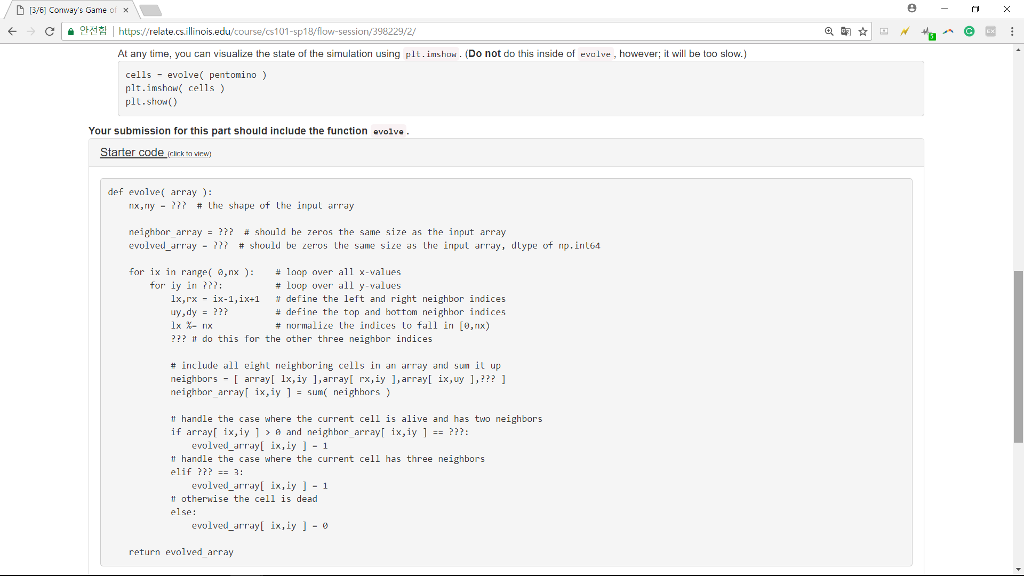
3yE] Conway's Game ofx ? C ? ??? https://relate.cs.illinois.edu/course/cs101-sp18 flow session 3%2292/ Conway's Game of Life 10 points Our example starting configuration will be the R-pentomino, If we were to apply this set of rules to evolve the prior snapshot forward one step at a time, the following sequence would result: Your first challenge is to evolve an array one step farward by applying the rules to each call. As a reminder, the rules are: 1. Any live cell with fewer than two live neighbours dies, as if subject to under-population. 2. Any live cell with two or three live neighbours lives to the next generation. 3. Any live cell with more than three live neighbours dies, as if subject to over-population. 4. Any dead cell with exacty three live neighbours becomes a live cell, as if by reproductio. Thus, we need only know the sum of the neighbors to detemine which cells live, which die, and which are bom Compose a function evalve array which accepts an ndarray named array, and returns the next evolution of that array. 1. We only noed to know the sum of the neighbors to determine which cells live and which die. (The diagonals are neighbors as well.) Find the rules and apply boundary conditions. For instance, what happens to boundary cells? Are they considered as not having neighbors (dead boundary) or as wrapping around (periadic boundary)? For simplicity in this case, we'll go with the periodic boundary. (But we still have to handle the edge cases separately.) To implement the periodic boundary condition, we need to check if an index would be out of bounds; if so, wrap it around. This is a modulus operation! Thus for the left neighbor index Ix this looks like 1x - ix-1 1xnx 2. We then apply the rules to determine the noxt generation. 3. Return the evolved cellular array evolved erray I will test the simulation using the following initial R-pentomino: pentomino-np.zeros48,48) pentomino 18,10-1 pentomino 9,1]1 pentominol 11,1-1 pentomino 18,9 -1 pentominol 9,11 ]1 plt.imshow pentomino) hod 3yE] Conway's Game ofx ? C ? ??? https://relate.cs.illinois.edu/course/cs101-sp18 flow session 3%2292/ Conway's Game of Life 10 points Our example starting configuration will be the R-pentomino, If we were to apply this set of rules to evolve the prior snapshot forward one step at a time, the following sequence would result: Your first challenge is to evolve an array one step farward by applying the rules to each call. As a reminder, the rules are: 1. Any live cell with fewer than two live neighbours dies, as if subject to under-population. 2. Any live cell with two or three live neighbours lives to the next generation. 3. Any live cell with more than three live neighbours dies, as if subject to over-population. 4. Any dead cell with exacty three live neighbours becomes a live cell, as if by reproductio. Thus, we need only know the sum of the neighbors to detemine which cells live, which die, and which are bom Compose a function evalve array which accepts an ndarray named array, and returns the next evolution of that array. 1. We only noed to know the sum of the neighbors to determine which cells live and which die. (The diagonals are neighbors as well.) Find the rules and apply boundary conditions. For instance, what happens to boundary cells? Are they considered as not having neighbors (dead boundary) or as wrapping around (periadic boundary)? For simplicity in this case, we'll go with the periodic boundary. (But we still have to handle the edge cases separately.) To implement the periodic boundary condition, we need to check if an index would be out of bounds; if so, wrap it around. This is a modulus operation! Thus for the left neighbor index Ix this looks like 1x - ix-1 1xnx 2. We then apply the rules to determine the noxt generation. 3. Return the evolved cellular array evolved erray I will test the simulation using the following initial R-pentomino: pentomino-np.zeros48,48) pentomino 18,10-1 pentomino 9,1]1 pentominol 11,1-1 pentomino 18,9 -1 pentominol 9,11 ]1 plt.imshow pentomino) hod