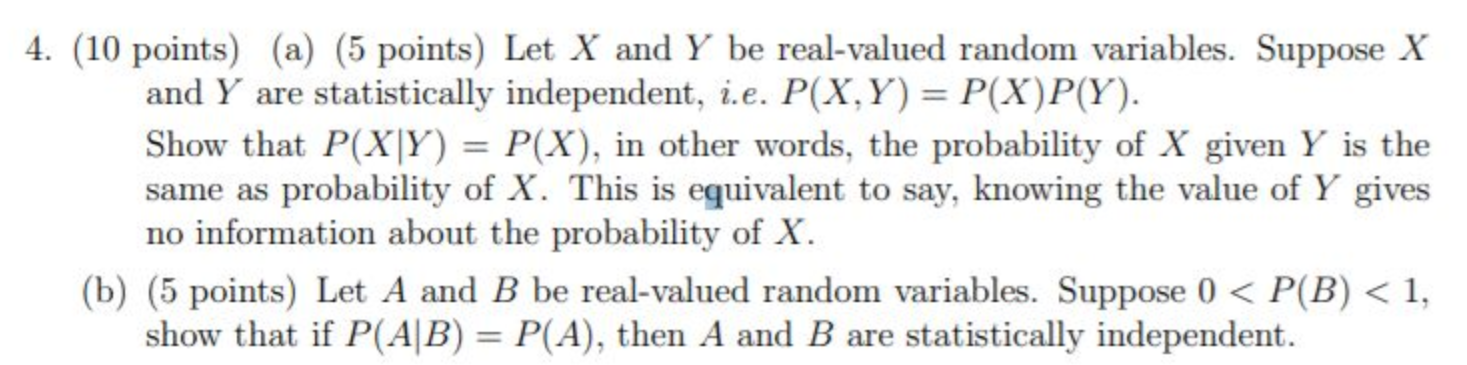
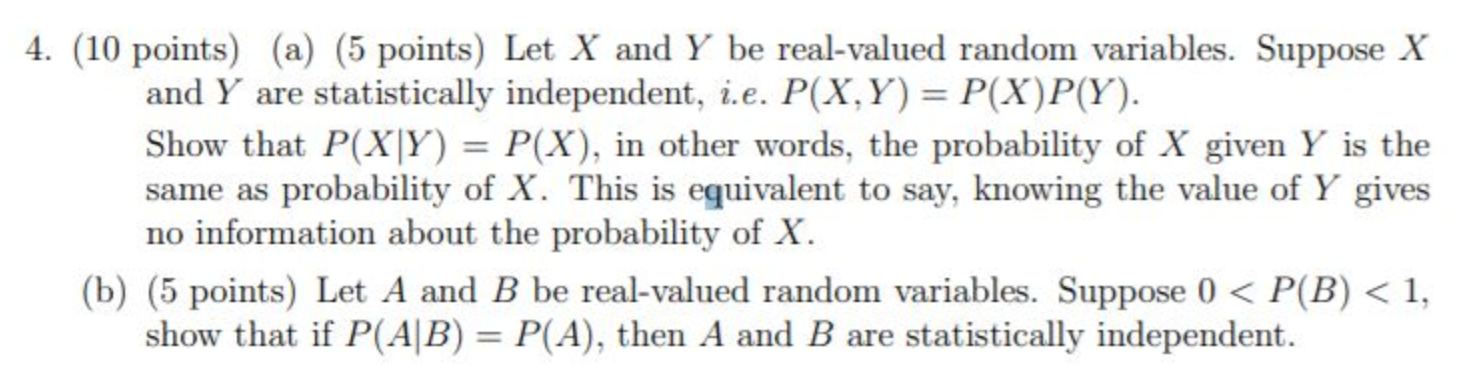
4. (10 points) (a) (5 points) Let X and Y be realvalued random variables. Suppose X and Y are statistically independent, i.e. P(X,Y) = P(X)P(Y). Show that P(X|Y) = P(X), in other words, the probability of X given Y is the same as probability of X. This is eguivalent to say, knowing the value of Y gives no information about the probability of X. (b) (5 points) Let A and B be real-valued random variables. Suppose 0