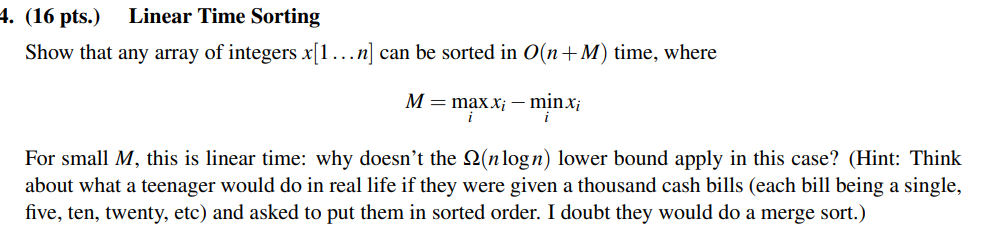
4. (16 pts.) Linear Time Sorting Show that any array of integers x[1... n) can be sorted in O(n+M) time, where M=maxxi minxi i For small M, this is linear time: why doesn't the 12(nlogn) lower bound apply in this case? (Hint: Think about what a teenager would do in real life if they were given a thousand cash bills (each bill being a single, five, ten, twenty, etc) and asked to put them in sorted order. I doubt they would do a merge sort.)