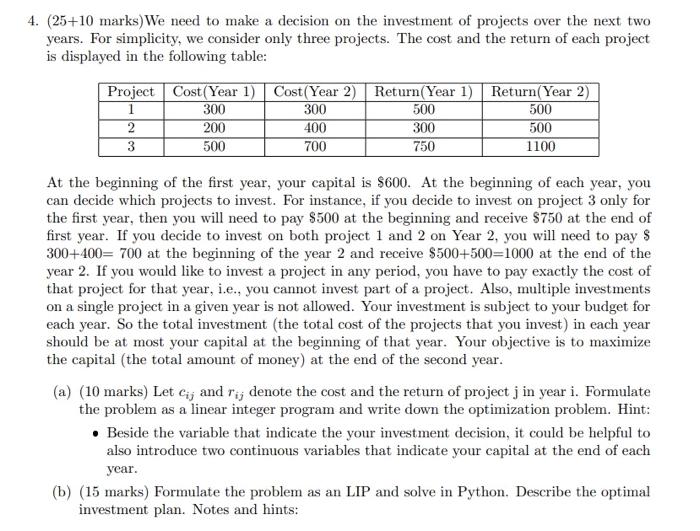
4. (25+10 marks) We need to make a decision on the investment of projects over the next two years. For simplicity, we consider only three projects. The cost and the return of each project is displayed in the following table: At the beginning of the first year, your capital is $600. At the beginning of each year, you can decide which projects to invest. For instance, if you decide to invest on project 3 only for the first year, then you will need to pay $500 at the beginning and receive $750 at the end of first year. If you decide to invest on both project 1 and 2 on Year 2 , you will need to pay $ 300+400=700 at the beginning of the year 2 and receive $500+500=1000 at the end of the year 2 . If you would like to invest a project in any period, you have to pay exactly the cost of that project for that year, i.e., you cannot invest part of a project. Also, multiple investments on a single project in a given year is not allowed. Your investment is subject to your budget for each year. So the total investment (the total cost of the projects that you invest) in each year should be at most your capital at the beginning of that year. Your objective is to maximize the capital (the total amount of money) at the end of the second year. (a) (10 marks) Let cij and rij denote the cost and the return of project j in year i. Formulate the problem as a linear integer program and write down the optimization problem. Hint: - Beside the variable that indicate the your investment decision, it could be helpful to also introduce two continuous variables that indicate your capital at the end of each year. (b) (15 marks) Formulate the problem as an LIP and solve in Python. Describe the optimal investment plan. Notes and hints: - Since Python counts from 0 instead of 1 , you can use year 0 to denote year 1 , and project 0 to denote project 1. - You can use cp.Variable(3, boolean=True) to denote a binary variable of size 3. - Beside the variable that indicate the your investment decision, it could be helpful to also introduce two continuous variables that indicate your capital at the end of each year. - The equality constraint in cvxpy is straight-forward. For instance, x+y=1 is coded as x+y==1. - You need to consider carefully the budget constraint at the beginning of the second year. c) (Bonus: 10 marks) Suppose that there is a bonus scheme that encourage investors to continue on investing the same project in the second year. To be more specific, if we invest on project i in the first year and continue to invest on this project in the second year, you would receive 100 dollar discount for the cost of project i in the second year. For instance, if we invest on project 1 on both years, the cost to pay at the beginning of the second year is just 200, instead of 300 . Reformulate the problem after considering this bonus scheme and resolve it in Python. What is the optimal investment plan now? Explain the intuition if the investment plan is different from the previous one