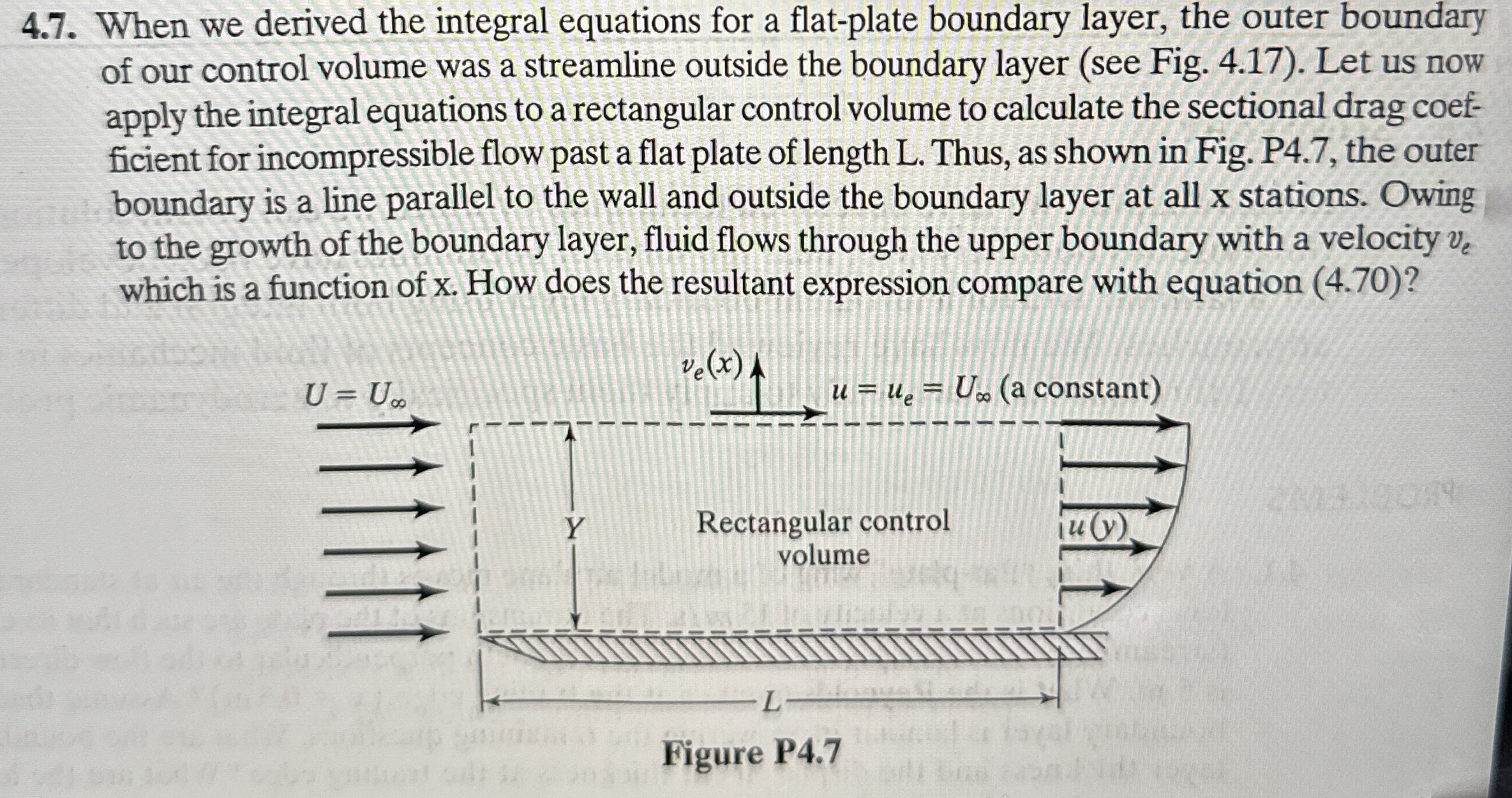
Question: 4 . 7 . When we derived the integral equations for a flat - plate boundary layer, the outer boundary of our control volume was
When we derived the integral equations for a flatplate boundary layer, the outer boundary of our control volume was a streamline outside the boundary layer see Fig. Let us now apply the integral equations to a rectangular control volume to calculate the sectional drag coefficient for incompressible flow past a flat plate of length L Thus, as shown in Fig. P the outer boundary is a line parallel to the wall and outside the boundary layer at all x stations. Owing to the growth of the boundary layer, fluid flows through the upper boundary with a velocity which is a function of x How does the resultant expression compare with equation
Figure P
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


