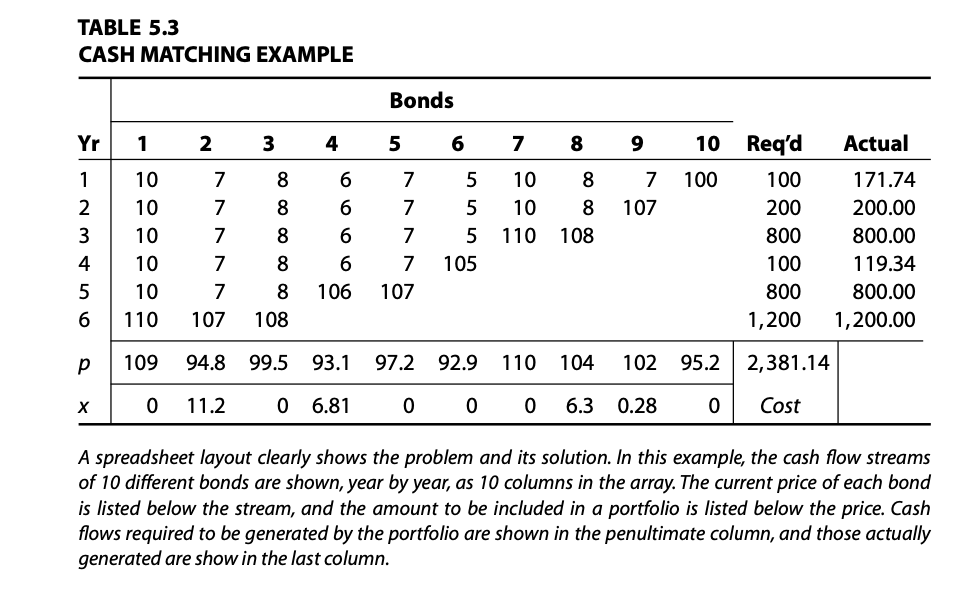
4. (Bond matrix ) The cash matching and other problems can be conveniently represented in matrix form. Suppose there are m bonds. We define for each bond j its associated yearly cash flow stream (column) vector cj, which is n-dimensional. The yearly obligations are likewise represented by the n-dimensional vector y. We can stack the c; vectors side by side to form the columns of a bond matrix C. Finally we let p and x be m-dimensional column vectors. The cash matching problem can be expressed as maximize px subject to Cx>y x>0. (a) Identify C,y,p, and x in Table 5.3. (b) Show that if all bonds are priced according to a common term structure of interest rates, there is a vector v satisfying c?v=p. = What are the components of v? (c) Suppose b is a vector whose components represent obligations in each period. Show that a portfolio x meeting these obligations exactly satisfies Cx=b. (d) With x and v defined as before, show that the price of the portfolio x is v b. Interpret this result. a Che Cash Matching Problem 003 2016 m 090 000 Zsobnu A simple optimal portfolio problem is the cash matching problem. To describe this problem, suppose that we face a known sequence of future monetary obligations . (If we manage a pension fund, these obligations might represent required annuity dos spayments.) We wish to invest now so that these obligations can be met as they occur 20 and accordingly, we plan to purchase bonds of various maturities and use the coupon payments and redemption values to meet the obligations. The simplest approach is to wyd by design a portfolio that will, without future alteration, provide the necessary cash as required. spolu nimpong To formulate this problem mathematically, we first establish a basic time period length, with cash flows occurring at the end of these periods. For example, we might U use 6-month periods. Our obligation is then a stream y=(1,72,...,Yn), starting one d period from now. (We use boldface letters to denote an entire stream.) Likewise each bond has an associated cash flow stream of receipts, starting one period from FOTO now. If there are m bonds, we denote the stream associated with one unit of bond j by c = (C1j, C2j, ..., Cnj). The price of bond j is denoted by Pj. We denote by x; Ed A the amount of bond ; to be held in the portfolio. The cash matching problem is to enor find the x;'s of minimum total cost that guarantee that the obligations can be met. Specifically, lubvibal oldog bud vobga can vd boxileum WOH.moldos Istiqoo on avlozon osa to stol og ud and to usmev nol moldog rignivoa dito minimize pixjul og budart olarad odlo j=1 m subject to Ecuri 2 yi for i=1,2,...,nismisqo s.2 j=1 e os veidong nonstique Tox; 20 for j=1,2,..., m. 1 a to dodatnog laro midt stato The objective function to be minimized is the total cost of the portfolio, which is 710 oi equal to the sum of the prices of the bonds times the amounts purchased. The main Biggs set of constraints are the cash matching constraints. For a given i the corresponding tamil must be at least equal to the obligation in period i. The final constraint rules out the b constraint states that the total amount of cash generated in period i from all m bonds possibility of selling bonds short. TABLE 5.3 CASH MATCHING EXAMPLE Bonds Yr 1 2 3 4 5 6 7 8 9 Actual -Nm 7 7 8 8 6 6 2 aaa 7 107 10 10 110 10 10 10 10 10 110 5 5 5 105 8 8 108 3 4 5 6 00 00 00 00 00 7 7 7 107 7 7 7 7 107 8 8 8 108 6 6 106 10 Req'd 100 100 200 800 100 800 1,200 171.74 200.00 800.00 119.34 800.00 1,200.00 109 94.8 99.5 93.1 97.2 92.9 110 104 102 95.2 2,381.14 0 11.2 06.81 0 0 0 6.3 0.28 0 Cost A spreadsheet layout clearly shows the problem and its solution. In this example, the cash flow streams of 10 different bonds are shown, year by year, as 10 columns in the array. The current price of each bond is listed below the stream, and the amount to be included in a portfolio is listed below the price. Cash flows required to be generated by the portfolio are shown in the penultimate column, and those actually generated are show in the last column. 4. (Bond matrix ) The cash matching and other problems can be conveniently represented in matrix form. Suppose there are m bonds. We define for each bond j its associated yearly cash flow stream (column) vector cj, which is n-dimensional. The yearly obligations are likewise represented by the n-dimensional vector y. We can stack the c; vectors side by side to form the columns of a bond matrix C. Finally we let p and x be m-dimensional column vectors. The cash matching problem can be expressed as maximize px subject to Cx>y x>0. (a) Identify C,y,p, and x in Table 5.3. (b) Show that if all bonds are priced according to a common term structure of interest rates, there is a vector v satisfying c?v=p. = What are the components of v? (c) Suppose b is a vector whose components represent obligations in each period. Show that a portfolio x meeting these obligations exactly satisfies Cx=b. (d) With x and v defined as before, show that the price of the portfolio x is v b. Interpret this result. a Che Cash Matching Problem 003 2016 m 090 000 Zsobnu A simple optimal portfolio problem is the cash matching problem. To describe this problem, suppose that we face a known sequence of future monetary obligations . (If we manage a pension fund, these obligations might represent required annuity dos spayments.) We wish to invest now so that these obligations can be met as they occur 20 and accordingly, we plan to purchase bonds of various maturities and use the coupon payments and redemption values to meet the obligations. The simplest approach is to wyd by design a portfolio that will, without future alteration, provide the necessary cash as required. spolu nimpong To formulate this problem mathematically, we first establish a basic time period length, with cash flows occurring at the end of these periods. For example, we might U use 6-month periods. Our obligation is then a stream y=(1,72,...,Yn), starting one d period from now. (We use boldface letters to denote an entire stream.) Likewise each bond has an associated cash flow stream of receipts, starting one period from FOTO now. If there are m bonds, we denote the stream associated with one unit of bond j by c = (C1j, C2j, ..., Cnj). The price of bond j is denoted by Pj. We denote by x; Ed A the amount of bond ; to be held in the portfolio. The cash matching problem is to enor find the x;'s of minimum total cost that guarantee that the obligations can be met. Specifically, lubvibal oldog bud vobga can vd boxileum WOH.moldos Istiqoo on avlozon osa to stol og ud and to usmev nol moldog rignivoa dito minimize pixjul og budart olarad odlo j=1 m subject to Ecuri 2 yi for i=1,2,...,nismisqo s.2 j=1 e os veidong nonstique Tox; 20 for j=1,2,..., m. 1 a to dodatnog laro midt stato The objective function to be minimized is the total cost of the portfolio, which is 710 oi equal to the sum of the prices of the bonds times the amounts purchased. The main Biggs set of constraints are the cash matching constraints. For a given i the corresponding tamil must be at least equal to the obligation in period i. The final constraint rules out the b constraint states that the total amount of cash generated in period i from all m bonds possibility of selling bonds short. TABLE 5.3 CASH MATCHING EXAMPLE Bonds Yr 1 2 3 4 5 6 7 8 9 Actual -Nm 7 7 8 8 6 6 2 aaa 7 107 10 10 110 10 10 10 10 10 110 5 5 5 105 8 8 108 3 4 5 6 00 00 00 00 00 7 7 7 107 7 7 7 7 107 8 8 8 108 6 6 106 10 Req'd 100 100 200 800 100 800 1,200 171.74 200.00 800.00 119.34 800.00 1,200.00 109 94.8 99.5 93.1 97.2 92.9 110 104 102 95.2 2,381.14 0 11.2 06.81 0 0 0 6.3 0.28 0 Cost A spreadsheet layout clearly shows the problem and its solution. In this example, the cash flow streams of 10 different bonds are shown, year by year, as 10 columns in the array. The current price of each bond is listed below the stream, and the amount to be included in a portfolio is listed below the price. Cash flows required to be generated by the portfolio are shown in the penultimate column, and those actually generated are show in the last column