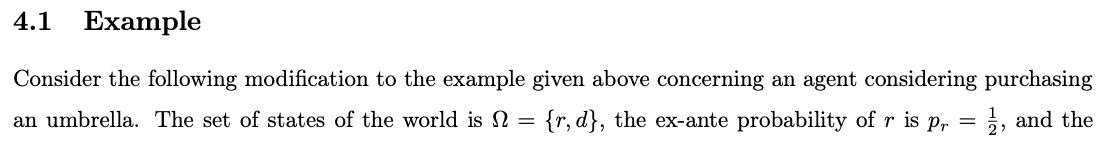
4. Consider a modified general equilibrium environment in which there are two possible states of the world, state w and state w, which are equally likely ex-ante. There are two kinds of goods, a and b. There are two expected utility agents, Agent 1 and Agent 2, whose Bernoulli utilities depend on the state of the world, as well as their ultimate ownership levels of the various goods. In particular, the Bernoulli utility u (w, x1,a, x1,b) of Agent 1 is given by u1 (w,x1,a,x1,b) = In(1+x1,a) if w= w [In(1+x1,6) if w = w. For some 0 4 Value of Information Suppose there is a finite set of states and that the probability distribution over states is p, with pw > 0 for each w. There is an expected utility agent who will choose some action x X and make some payment t = R. The set of outcomes is Z = {(w, x, t) : w N x X, t R+}. For every (w,x) = N X the agent's Bernoulli utility u(w, x, t) is strictly decreasing in t R+. = The agent can choose to purchase an information structure (, S) at price R+, where S {1, ..., SN} is a finite set of signals [sn]w] gives the conditional probability of signal s given state w, and, for every 1 n N, [sn|w] > 0 for some w N. For every 1 n N, let Pp,o,s[$n] Pwo[SnW = be the ex-ante probability of signal sn occurring. Observe that Pp,o,S[Sn] > 0 for all 1 n N. Additionally, for every (w, sn), let Pp,o,s[w|Sn] = Pw [8n|w] Pp,o,S[sn] be the conditional probability the agent would assign to state w upon the agent purchasing the information structure and observing signal sn. max xX (, , 0). Let Vno info be the corresponding value to the agent. If the agent does purchase the information structure at price R+, then their problem is effectively max x1,...,xNEX [sn|w]u(w, In,). Let Vinfo(T) be the corresponding value to the agent. = Vno info. The agent's highest willingness to pay 7 for the information structure satisfies Vinfo(T) For all, the agent would strictly prefer to purchase the information structure over not purchasing the information structure. For all > , the agent would strictly prefer to not purchase the information structure over purchasing the information structure. For = , the agent would be indifferent between purchasing the information structure and not purchasing the information structure. Note that, for all ER+ and x1,...,xN X, Thus, [[ Pwo[Sn\w]u(w, xn, ) = PwO [Sn\W]U(W, Xn,), = [ [ Pw' [Sn|W'] [ ' Pw [Sn\w] w'EN Pw' [Sn|w'] => Pp,o,s[$n] > Pp,o,S[W|Sn]U(W, Xn,). n Vpurchase (T) = Pp,o,S[Sn] Pp,o,S[W| Sn]U(w, x, ), where, for each 1 n N, x* X solves n w -u (w, xn, ), max xX Pp,o,S[W|Sn] U(W, X,), which would be the agent's problem if they were to purchase the information structure at price R+, observe signal sm, and update to the relevant conditional probability distribution. 4.1 Example Consider the following modification to the example given above concerning an agent considering purchasing an umbrella. The set of states of the world is = {r, d}, the ex-ante probability of r is pr = , and the ex-ante probability of d is pd = . Moreover, X = {u, n}. The agent's Bernoulli utility u satisfies and u(w, u,t) = -10 - t -22 t if w=r, u(w, n,t) = -t if w = d for all (w, t). In the absence of an informative information structure, the agent would choose to purchase an umbrella, since doing so would result in an expected utility of -10, which is strictly greater than -11, the expected utility the agent would obtain from not purchasing an umbrella. Thus, here Vno info = 10. Suppose that the agent can purchase at price = R+ an information structure (, S), in which S = {a,b}, [ar] = [b]d] = , and o[b]r] = [a]d] = . Note that, with such an information structure, the probability of signal a occurring is Pp,o,s = - and the probability of signal b occurring is Pp,,,S = . Moreover, under such an information structure, the conditional probability of the state being r given signal a is Pp,o,s[r|a] Pro[ar] Pp,o,s[a]' 3 4' and the conditional probability of the state being d given signal a is Pp,o,S[r|a] = Pa [a\d] Pp,o,s[a]' = 4' so the conditional probability distribution over states given signal a is 1/18, + 1d. Similarly, the conditional probability distribution over states given signal b is 18, + 1/8d. Given signal a, purchasing an umbrella would induce probability distribution over outcomes 1/18 (r,u,) + 1/18 (d,u,) and thus give the agent expected utility 3 1 Epurchase [u(w, x, t)|a] = {u(r, u, ) + u(d, u, ) = =-10-, while not purchasing an umbrella would induce probability distribution over outcomes 12/16 (r,n,) + 1/18 (d,n,)