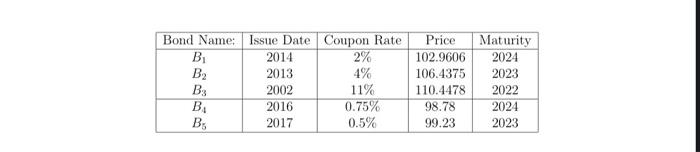
4. Finance Applications: Bond pricing and Arbitrage Consider a set of (B1, B2, B3,B4, Bs) German Bunds with maturity exactly three years from now with different coupon rates. Notice new bonds are paying low coupon rates while old bonds pay higher rates since those were set during different interest rate environments. For simplicity assume today is January 1st, 2021 and that all bonds have a face value of 100 Euros. They pay out 100 euros plus the coupon at the maturity. (See also the tables above) The future cash flows for these bonds in years 2022 2023 and 2024 can be summarized as (a) Consider the cash flows for B1, B2, B3 as matrix M and P are the prices let d be a vector, then the prices of the bonds solve a set of equations Md = P Price today CF2022 CF2023 CF 2024 102.9606 2 2 102 106.4375 4 104 0 110.4478 111 0 0 98.78 0.75 0.75 100.75 99.23 0.5 100.5 0 Compute the inverse of M (b) Solve for d (c) Consider Bund contracts B., Bs. Write a new version for M including all five bond contracts. There does not exist a solution for d. Explain. (d) Given the original M, solve for the correct fair price for B, and B.. (e) If B, were correctly priced what combination of bonds B1, B2, B, can replicate B (derive the linear combination) write this out in matrix notation. 2% 2023 Bond Name: Issue Date Coupon Rate Price Maturity B 2014 102.9606 2024 B2 2013 4% 106.4375 B: 2002 11% 110.4478 2022 B 2016 0.75% 98.78 2024 . 2017 0.5% 99.23 2023