Question: 4. For an integrable random variable , we have by dominated convergence that limrE[;>r]=E[limr1{>r}]=E[0]=0. For a family of random variables {t;tT}, we call it uniformly

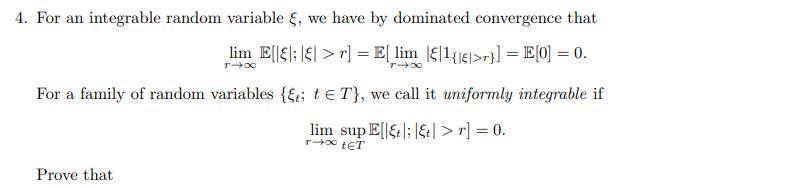
4. For an integrable random variable , we have by dominated

convergence that limrE[;>r]=E[limr1{>r}]=E[0]=0. For a family of random variables {t;tT}, we call

4. For an integrable random variable , we have by dominated convergence that limrE[;>r]=E[limr1{>r}]=E[0]=0. For a family of random variables {t;tT}, we call it uniformly integrable if limrsuptTE[t;t>r]=0 Prove that (b) if there exists a function G:R+R+which is increasing and such that G(x)/x as x and suptTE[G(t)]r]=E[limr1{>r}]=E[0]=0. For a family of random variables {t;tT}, we call it uniformly integrable if limrsuptTE[t;t>r]=0 Prove that (b) if there exists a function G:R+R+which is increasing and such that G(x)/x as x and suptTE[G(t)]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

connect" 1 8 4 8 5 Operational Decisions: Bump Up Your Bumper Location: 1 0 0 % Layout This seems like an easy decision. Which drawback of this location would even make us consider the other two...

an operation that yields a N aN value when neither of its arguments is a N aN, (b) an operation with finite arguments that yields +, (c) an operation with an argument + that yields a finite result....

These are the problems to solve. 1. Let X and Y be independent and uniform on {1, . .., 5}. Find a) the conditional distribution b) the conditional expectation of X given X - Y = 1.5. Let (Xn) be a...

You may use the points below. If {i : i = 1,2, ... } is a family of integrable random variables such that i + 0 almost surely as oo and limi* Ei 0, is the family {&i : = 1, 2, ... } uniformly...

Let $\left\{X_{n}ight\}_{n=1}^{\infty}$ be a sequence of random variables such that $P\left(\left|X_{n}ight| \leq Yight)=1$ for all $n \in \mathbb{N}$ where $Y$ is a positive integrable...

2 . ( a ) Let Z be an integrable random variable and G F be a sigma algebra. Show that EP [ jZj jG ] > = j EP [ Z jG ] j: ( b ) Let Z be an integrable random variable and define Zt : = EP [ ZjFt ] ....

=+25.19. In the applications of Theorem 9.2, only a weaker result is actually needed: For each K there exists a positive a = a(K) such that if E[X]- 0, E[X2] =1, and E[X4] K, then P[X 2 0] 2 @....

5. Let Y be an integrable random variable on a probability space (0, F, P) and let G be a sub-o-algebra of F. Based on the information in 9, we can form the estimate E[Y G] of Y and define the error...

13. Show that a collection K of random variables X is UI if sup P(|X| 2 x) 13. Show that a collection K of random variables X is UI if sup x) S P(IYI x) XeK for all x e R, where Y is an integrable...

Chebyshev's inequality gives a relation between the fraction of values that can be found a certain distance away from the mean. Let X be an integrable random variable such that E [ X] is finite and...

5. Let X, X2,..., Xn be integrable random variables (i.e., EX n} = 0 otherwise. 7. Let X, X2 be independent exponentially distributed random variables, with densities fi(x) = Ae-1 and f2(x) = 2e-2...

Harpo Enterprises, Inc. wants to raise $33 million by issuing 12-year, zero coupon bonds. The market requires an 6.0 percent return on similar bonds. The face value per bond will be $1,000. How many...

If you were considering buying stock in a company, would you support rigorous (and potentially expense) financial accountability such as that called for by Section 404 of Sarbanes-Oxley? Why or why...

What was the status of the majority of entertainers and athletes in the Roman world? Condemned criminals Amateur aristocrats Professional slaves Amateur poor Professional poor Amateur sisves...

provide a complete mechanism and the structures 1 - methylcyclopentane reacts with cl 2 in CH 2 Cl 2

To exacerbate the processing of your US tax return, use the mailing label and bar coded envelope that comes with your tax package.

What benefits does effective communication give you and your organization? [LO-1]

Albert Edmunds and me are Owners of the real estate firm of Edmunds & Cale, which have recently opened a new office in San Diego co.