4) Gaussian functions are used as test functions to solve for the hydrogen atom.
a) Find the variational solution for the hydrogen atom using two Gaussian functions.
b) Discuss the results obtained in terms of the wave function, probability function, and energy.
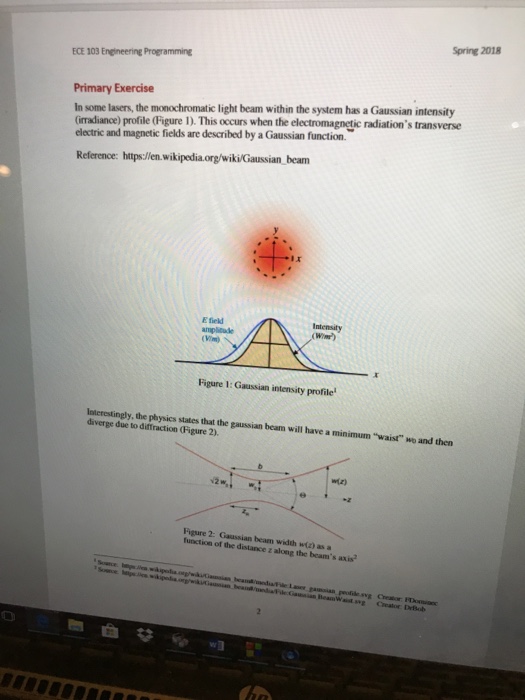
It's are not allowed. Please do write in such a way that we we points to unintelligible scribbles. problems on three pages. In total you can earn with this part of the test 60 points. Points are assigned as indicated. There are sis Please read this notice: START EACH PROBLEM ON A NEW PAGE Problems: 1. (15) A projection X-ray imaging system is set up as shown in Figure I. All length units are in cmn. Object Source W z = 40/ /Detector d = 60 Figure | Projection radiography system problem 1. Assume that the total system response can be described by the following convolution: L(x,, VJ) = Ks(x, / m. y. Im).(x, IM, y,IM) . where xy denote coordinates in the detector plane, K is a constant, s(x, y) denotes the X-ray source distribution and /(xy) is the spatial transmission function of the object whose thickness we ignore, and i and M are the source and object magnification, respectively. Assume that the X-ray source can be described as a ID Gaussian function: s(x, y) = Sge 6(y) (a) (5) Compute the object magnification M/ and the source magnification m. Answer Object magnification M = Sze image size object 3 40 50 = 1.5 Source magnification follows from placing a pinhole at the position of the object, source diameter D, imaged via pinhole at image plane diameter D': D -D' D' d- z D D -=1-M = -0.5 Z An ideal line phantom is to be imaged by the system, whose transmission function is given by:(b) (3) Determine the image of the phantom on the detector plane. First Berme Because: And: We obtain: Similar The image of the phantom consists of two Gaussian functions centered al- wild respectively WN with a variance equal to " (e) (3) Determine the minimal value of w such that the images of the two lines on the detector plane can be distinguished from each other. Answer The distance between the two peaks is: wif. The two peaks can be distinguished if the FWHM (Full Width at Half Maximum). The FWHW equals 2/mlvlog, 2 . Thus the minimal value of w = My Vlog, 2=0.35 cmSpring 2018 ECE 103 Engineering Programming Primary Exercise In some lasers, the monochromatic light beam within the system has a Gaussian intensity (irradiance) profile (Figure 1). This occurs when the electromagnetic radiation's transverse electric and magnetic fields are described by a Gaussian function. Reference: https://en.wikipedia.org/wiki/Gaussian_beam E field Intensity Figure 1: Gaussian intensity profile Interestingly, the physics states that the gaussian beam will have a minimum "waist" we and then diverge due to diffraction (Figure 2). 12 Figure 2: Gaussian beam width wir) as a function of the distance I along the beam's axis A Trator Dreich
