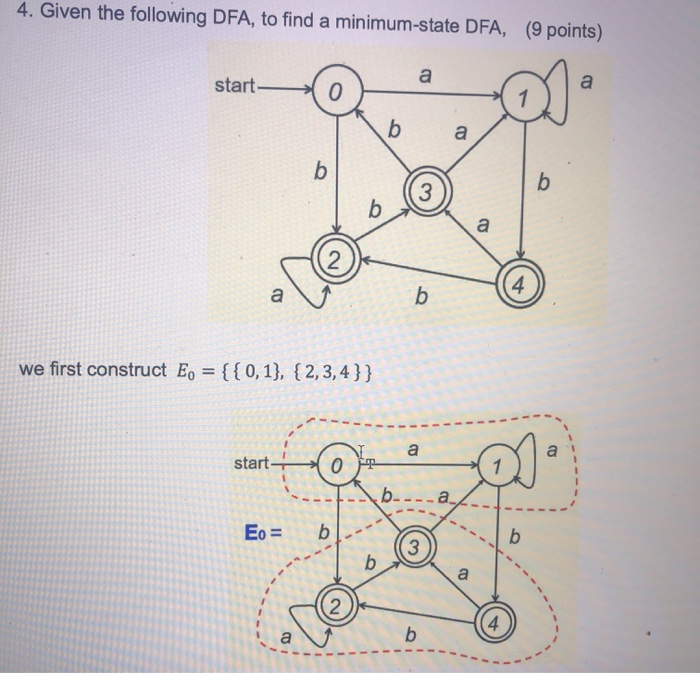
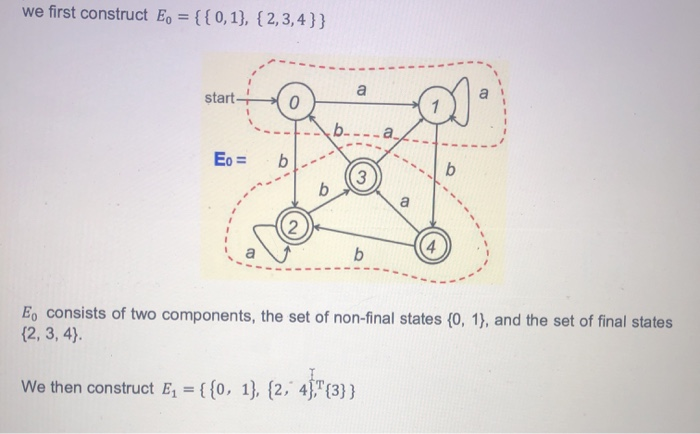
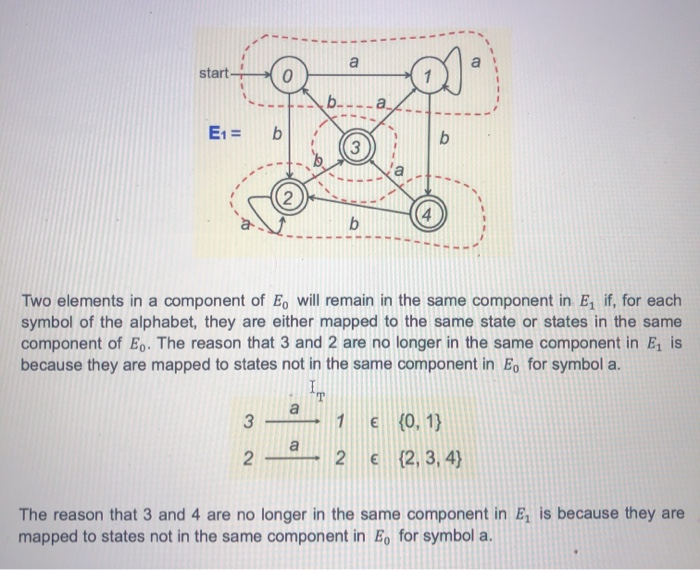
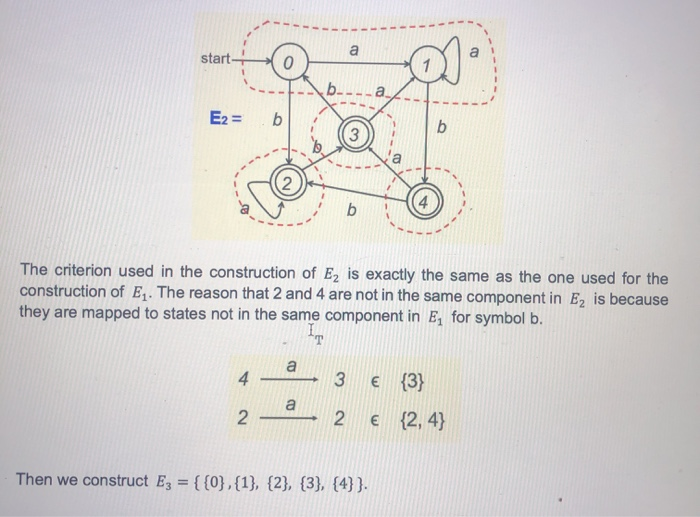
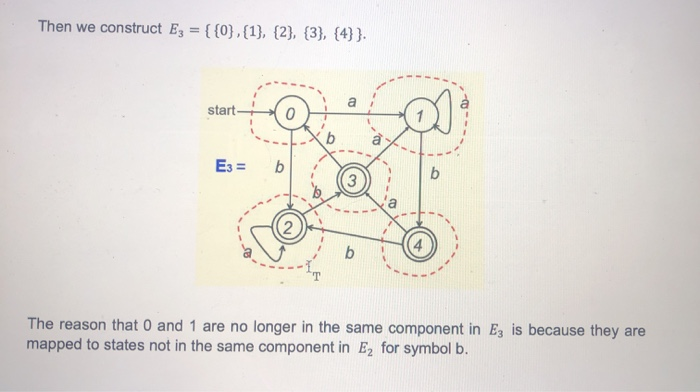
4. Given the following DFA, to find a minimum-state DFA, (9 points) start we first construct E, = {{0,1}, {2,3,4}} start on a ---- Eo = (13) b we first construct E, = {{0,1}, {2,3,4}} start to ---- Eo = bl E, consists of two components, the set of non-final states {0, 1}, and the set of final states {2, 3, 4). We then construct Ez = {{0, 1}, {2, 4}"{3}} 1. b- b Two elements in a component of E. will remain in the same component in E if, for each symbol of the alphabet, they are either mapped to the same state or states in the same component of En. The reason that 3 and 2 are no longer in the same component in E is because they are mapped to states not in the same component in E. for symbol a. 1 {0, 1} {2,3,4} The reason that 3 and 4 are no longer in the same component in E is because they are mapped to states not in the same component in E. for symbol a. Two elements in a component of E, will remain in the same component in E, if, for each symbol of the alphabet, they are either mapped to the same state or states in the same component of En. The reason that 3 and 2 are no longer in the same component in E is because they are mapped to states not in the same component in E, for symbol a. - {0, 1} 2 1 2 E a {2,3,4} The reason that 3 and 4 are no longer in the same component in Eis because they are mapped to states not in the same component in E, for symbol a. 1 3 {0, 1} {2,3,4} Next we construct Ez = {{0,1}, {2}, {3}, {4}} The criterion used in the construction of Ez is exactly the same as the one used for the construction of E. The reason that 2 and 4 are not in the same component in Ez is because they are mapped to states not in the same component in E for symbol b. a - 3 2 {3} {2,4} - Then we construct Ez = { {0},{1}, {2}, {3}, {4}}. Then we construct Ez = {{0},{1}, {2}, {3}, {4} }. start 0 E3 = b The reason that 0 and 1 are no longer in the same component in Ez is because they are mapped to states not in the same component in Ez for symbol b. 2 4 {2} {4} Since each component in Ez has one element only, it cannot be further reduced, i.e., if we construct Ex, it will be exactly the same as Ez. Hence, we stop the refining process and the states of the minimum-state DFA are: (5 points) The start state is: (2 point) The final states are: (2 points)