Question: Let b > 0 and f : R R be defined by f(x) = 6. (a) If f'(0) exists, then (Fill in the blanks)

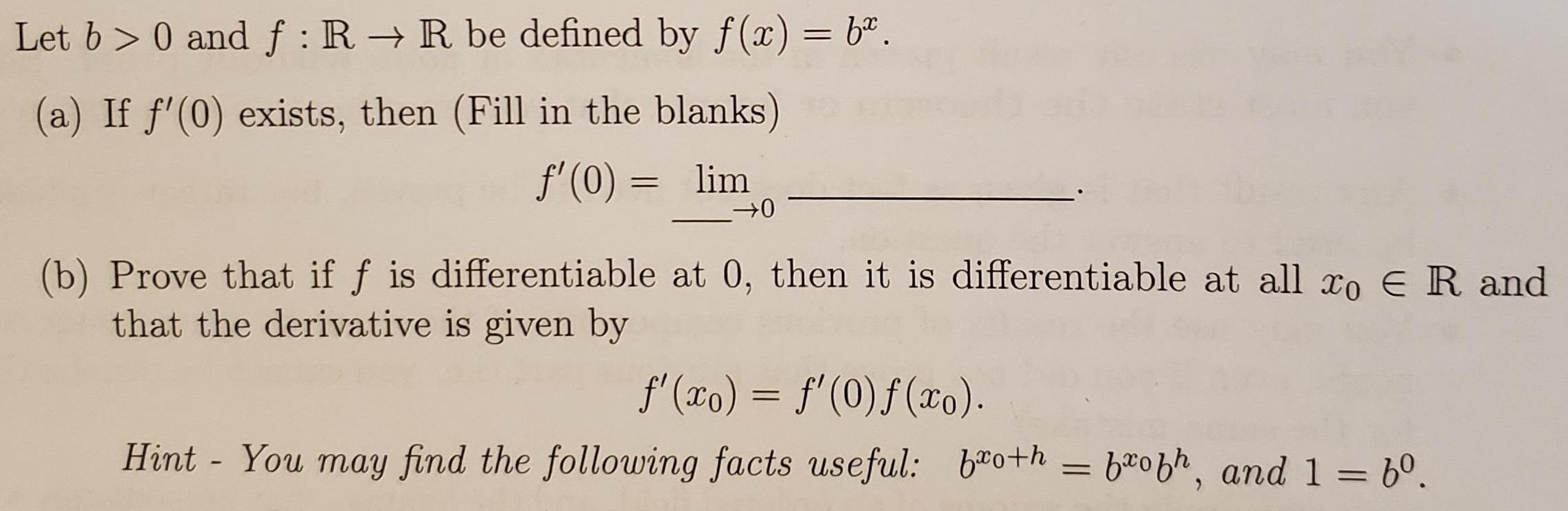
Let b > 0 and f : R R be defined by

Let b > 0 and f : R R be defined by f(x) = 6". (a) If f'(0) exists, then (Fill in the blanks) f'(0) = lim (b) Prove that if f is differentiable at 0, then it is differentiable at all xo E R and that the derivative is given by f'(xo) = f'(0)f (xo). %3D Hint - You may find the follouwing facts useful: beoth = brobh, and 1 = 6. %3D

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

4Explanation 1 we have byo and IRIR be defined by fx b... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Fill in the blanks in the following table of GDPstatistics: 2005 2006 2007 13,843 Nominal GDP 12,434 Real GDP 11,003 11,319 GDP deflator 116.6 119.7

Fill in the blanks in the following table: Cation Ai Formla Name Lithium oxide FePO4 3- Al2(SO4)3 Copper(II) nitrate Cr3+ MnCIO2 Ammonium carbonate Zinc perchlorate

Fill in the blanks in the following diagram representing sucrose synthesis in plants. UDP-glucose UDP H2O Sucrose

YORK UNIVERSITY SC/MATH 1019 3.0 D WRITTEN ASSIGNMENT #2 1. (5+5 points) (a) Prove that log(pm + 1) is O(log r) for all m e Et. (b) Give as good a big-O estimate as possible (in terms of the standard...

Question 14 0.5/1 pt ) 99 99 0 Details Score on last try: 0.5 of 1 pts. See Details for more. Get a similar question You can retry this question below Let F(x) = f(f(x)) and G(x) = (F(2)). You also...

2 + + Find the constant c so that lim $ exists. For that value of 0, determine the limit. (Hint: Find the value of c for which x 6 is a factor of the numerator.) x>Gx -11x+30

2. [-/2 Points] DETAILS SESSCALC2 10.5.004. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find a vector equation and parametric equations for the line. (Use the parameter t.) The line through the point...

(a) Let x 1 = 0, x 2 = 1. Find the unique linear function f(x) = ax + b that has the sample vector f = (3, 1) T . (b) Let x 1 = 0, x 2 = 1, x 3 = 1. Find the unique quadratic function f(x) = ax 2 +...

5.7 We have a population in which p(X=0)=.8 and p(X=1)=2. Let =p(X= 1) and 1=p(X=0). (a) (i) Calculate the population mean, X, and variance, X [E(X) and var(X)]. Note that var(X)=E(X2 )[E(X)]2 and...

An investor owns $3,000 of Adobe Systems stock, $6,000 of Dow Chemical, and $7,000 of Office Depot. What are the portfolio weights of each stock?

Draw an Activity diagram for webkiosk portal.

Does travel insurance Cover medical expenses? If So , under what circumstances? Provide example Does auto insurance cover medical expenses? If so , under what circumstances? Provide examples.

Q#3: The area show below in figure 2 is uniformly loaded. Given that q = 150KN/m2. Find the following Parameters at point A. Write ONLY the ANSWERS to the front of UNKNOWN PARAMETERS. [CLO2]_(4) S m...

Assume the ASX 500 forward earnings yield is 3 percent and the 10-year T-note yield is 5 percent. How are stocks valued according to the Fed model? a. Undervalued b. Fairly valued c. Over valued

The note below is an extract from the 2018 financial statements of Mercury Energy Limited, a New Zealand energy company. Required:? a) In the note above, some of Mercury?s hedges are designated as...

The equilibrium constant at 427 C is K = 9.4 x 10-5 . Calculate the value of G for the reaction at this temperature. R = 8.314 J/mol K N2(g) + 3H2(g) 2NH3(g) Chemistry

Calculate equity IRR for an LBO with the following assumptions. Entry EBITDA 300.0 Acquisition EBITDA multiple 11.0 x Debt financing, entry 1,600.0 Investment time horizon, years 4.0 Exit EBITDA...

tch the location in the body with the name of the bone. Location Bone Thigh bone --Click to select-- Lateral lower leg bone --Click to select-- Medial lower leg bone --Click to select-- Knee cap...

9 (i) Let b 0 and b 1 be the intercept and slope from the regression of yi on xi, using n observations. Let c1 and c2, with c2 0, be constants. Let b 0 and b 1 be the intercept and slope from the...

Please tutors guide me on this question Consider the algebraic transpose IT : Yf - Xy associated with the linear operator L : X - Y, where X and Y are linear vector spaces and Xy and Yf are their...

10 Let b 0 and b 1 be the OLS intercept and slope estimators, respectively, and let u be the sample average of the errors (not the residuals!). (i) Show that b 1 can be written as b 1 5 b1 1 i n wiui...

(i) Let b^ 0 and b^ 1 be the intercept and slope from the regression of yi on xi , using n observations. Let c1 and c2, with c22 0, be constants. Let b &0 and b &1 be the intercept and slope from the...

6 Let A 1 0 1 2 1 0 1 2 2 3 2 DONN and let b 0 1 0 a Find the rref A b Find the rank of A c Find a such that b is in the column space of A

please explain each step clearly (working and explanation) thank you!! 3. Gold Coats A. Right Circular Cylinder Let b > 0 be a constant real number. Create a right cylinder by revolving the line y=b...