Question: 4. Let T be an arbitrary rooted tree, where each vertex is labeled with a positive integer. A subset S of the nodes of

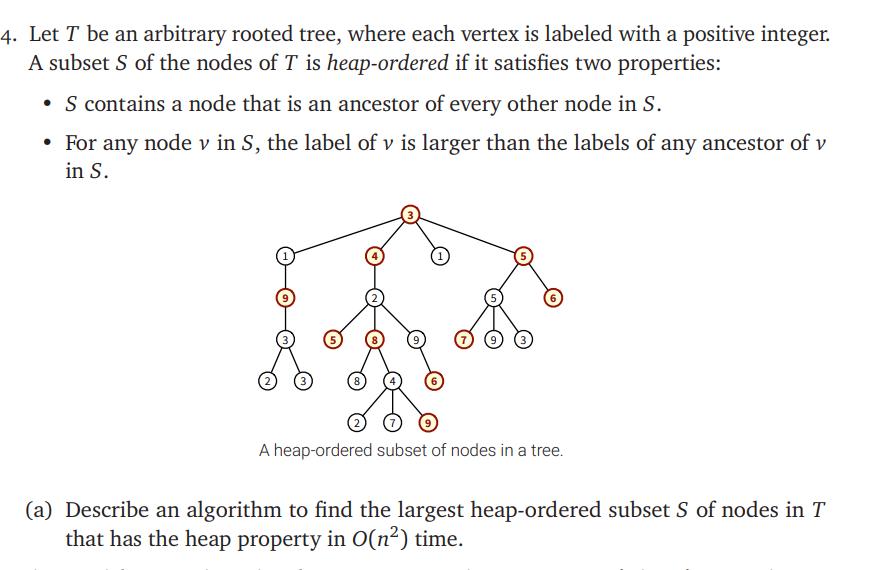
4. Let T be an arbitrary rooted tree, where each vertex is labeled with a positive integer. A subset S of the nodes of T is heap-ordered if it satisfies two properties: S contains a node that is an ancestor of every other node in S. For any node v in S, the label of v is larger than the labels of any ancestor of v in S. A heap-ordered subset of nodes in a tree. (a) Describe an algorithm to find the largest heap-ordered subset S of nodes in T that has the heap property in O(n) time.

Step by Step Solution

★★★★★

3.37 Rating (147 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The problem youve presented involves finding the largest heapordered subset S of nodes in a given tree T The heapordered property means that for a sub... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

On 9 March the value of GBP vs USD was 1.31 USD/GBP. 10 days later, on 19 March it plunged dramatically to 1.1437 USD/GBP. 11 days later, on 30 March, GBP appreciated to 1.24. Please explain...

Suppose we are given an n-node rooted tree T, such that each node v in T is given a weight w(v). An independent set of T is a subset S of the nodes of T such that no node in S is a child or parent of...

Let G = (V, E) be a directed graph in which each vertex u V is labeled with a unique integer L(u) from the set {1, 2,..., |V|}. For each vertex u V, let R(u) = (v V : u v) be the set of vertices...

Let's say there are only two countries in the entire world, Argentina and Chile, and there is free trade between them. The aggregated investments in both countries are ^A and I^C that are both...

In this question assume that p and q are atomic formulae. (a) Compare and contrast path formulae and state formulae in temporal logic. [4 marks] (b) Describe and contrast the meanings of F(G p) and...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

DETAILS What is the maximum segment length of a 100Base-FX netdwork, The last character ('X', etc) refers to the line code method used. Line code is a patdtern of voltage, current or photons used to...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Problem 10 We define the height h(T) of a full binary tree T recursively. Basis Step: The height of the full binary tree T consisting of only a root r is h(T) = 0. Recursive Step: If T 1 and T 2 are...

Problem 6: Draw all of the full and balanced binary trees formed by 0, 1, 2, and 3 applications of the recursive step of the recursive definition above. We define the height h(T) of a full binary...

Motivation is critical within every organization and every facet of life. In business, it involves every sub-division, it affects productivity, it aids in the setting and achievement of goals, it...

Determine the polar second moment of area of the propeller shaft cross-section shown in Fig. 38.23.

Evaluate: 4 x 8 x 3 - 4 x d x

A charged parallel-plate capacitor (with uniform electric field E = E z) is placed in a uniform magnetic field B = B x, as shown in Fig. 8.6. 3 (a) Find the electromagnetic momentum in the space...

Pension Worksheet) The following data relate to the operation of Kramer Co.s pension plan in 2011. The pension worksheet for 2010 is provided in P20-10. Service cost $59,000 Actual return on plan...

A long cable carries current in one direction uniformly distributed over its (circular) cross section. The current returns along the surface (there is a very thin insulating sheath separating the...

(a) Through what potential difference does an electron have to be accelerated, starting from rest, to achieve a speed of 0.980c? (b) What is the kinetic energy of the electron at this speed? Express...

The sun produces energy by nuclear fusion reactions, in which matter is converted into energy. By measuring the amount of energy we receive from the sun, we know that it is producing energy at a rate...

Which of the following is not a step toward purchasing an automobile?Multiple ChoiceShop for financingDetermine affordabilityMake a preliminary offerAnalyze needs versus wants

Using Figure 6.2 as a model, illustrate the operation of MAX-HEAPIFY (A, 3) on the array A = ?27, 17, 3, 16, 13, 10, 1, 5, 7, 12, 4 8, 9, 0?. Figure 6.2 16 16 3 2 3 10 14 10 4 5 6. 5 6. 14 9. 3. 9 10...

Consider the following multithreaded pseudocode for transposing an n Ã n matrix A in place: Analyze the work, span, and parallelism of this algorithm. P-TRANSPOSE(A) 1 n = A.rows 2 parallel...

Argue that in every n-node binary search tree, there are exactly n - 1 possible rotations. Figure 13.3 An example of how the procedure LEFT-ROTATE (T, x) modifies a binary search tree. In order tree...

For the burger joint contest described in Exercise 4, how will you combine components to model a trial? What is the response variable? Exercise 4 Your local burger joint gives away a game piece with...

Major League Baseball tests players to see whether they are using performance-enhancing drugs. Officials select a team at random, and a drug-testing crew shows up unannounced to test all 40 players...

A proud legislator claims that your state's new law banning texting and hand-held phones while driving reduced occurrences of infractions to less than 10% of all drivers. While on a long drive home...