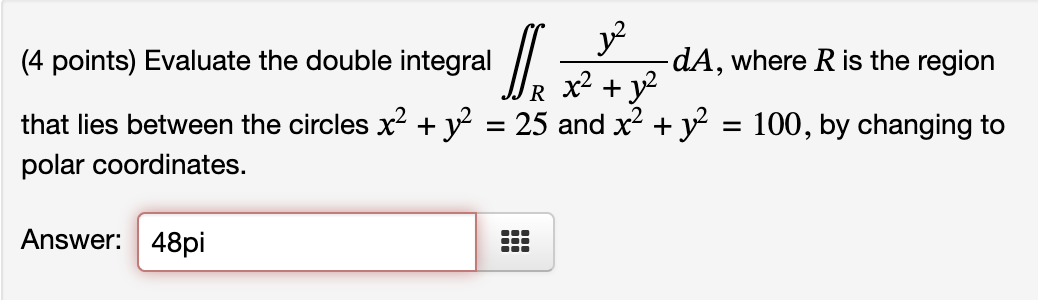
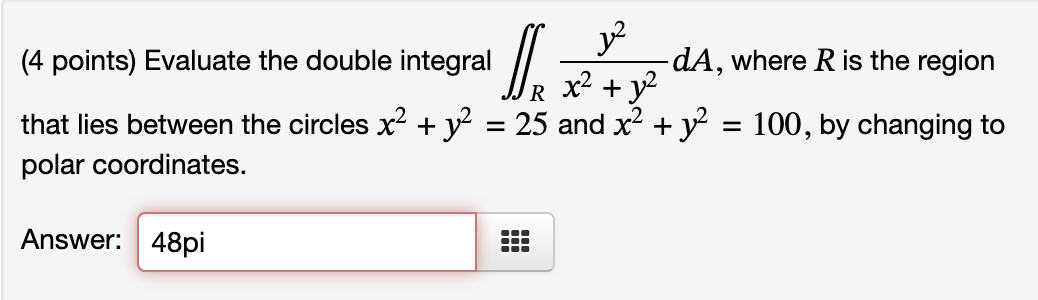
(4 points) Evaluate the double integral dA, where R is the region JJR X2 + 12 that lies between the circles x2 + y = 25 and x2 + y = 100, by changing to polar coordinates. Answer: 48pi(5 points) Evaluate the integral sin(x) dx dy by reversing the order of integration. With order reversed, b d sin(x ) dy dx, a C where a = , b = C = , and d = Evaluating the integral, So Jy sin(x2) dx dy = 1/(2)(-cos(4)+1)