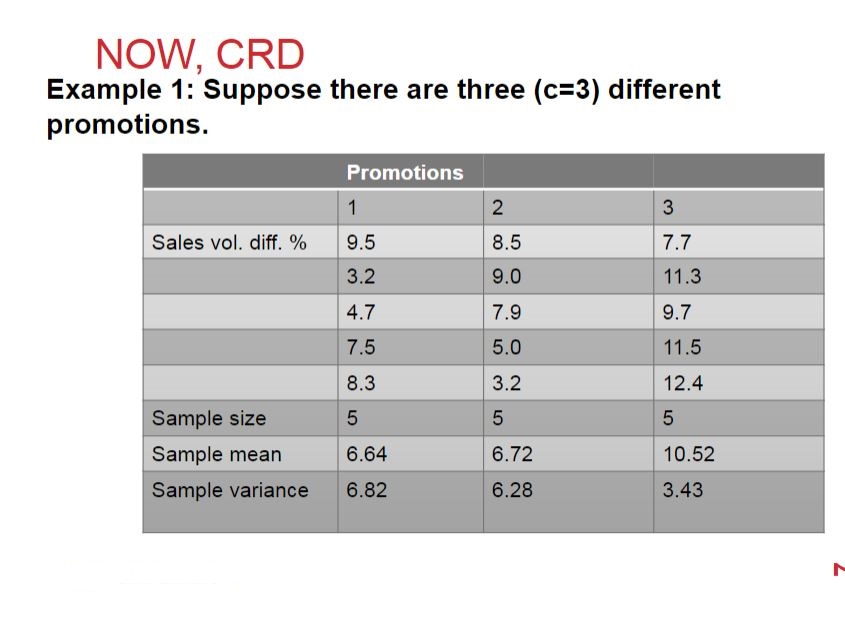
Question: 4. Recall the class note example on three promotions and sales volume difference percentage data; see Lecture 4-2.pdf lecture slide, page 7. Perform one-way ANOVA
4. Recall the class note example on three promotions and sales volume difference percentage data; see Lecture 4-2.pdf lecture slide, page 7. Perform one-way ANOVA procedure to test H0 : 1 = 2 = 3, vs. H1 : Not H0 . (a) Carry this out via hand calculations (it is worth doing this practice at least once!). (b) Now, do it again via statistical software package and compare with the result in (a). Remarks. We recall some logic behind ANOVA and also follow-up on the in-class questions. A One-Way Analysis of Variance is a way to test the equality of three or more means at one time by using variances. There are the between group variation (SSB) (not variance yet) and the within group variation (SSW). The whole idea behind the ANOVA is to compare the ratio of between group variance (that is, variation/degrees of freedom, similar to sample variance formula s 2 ) to within group variance (SSW/degrees of freedom). I agree to some extent that the term 'between-group' variation is a misnomer. This is because SSB does not measure something like (Xi Xj ) 2 , which seems to be more consistent with the term 'between-group' variation. However, notice that under the null H0, all means are the same (1 = 2 = 3). To test this equality of three (or more) means simultaneously, one wants to measure an aggregated variation caused by each group effect (that is, deviation from the overall mean); if this number is large enough, then it is an evidence that goes against H0. If the variance caused by the between group effect (that is, due to Xi X(overall mean), i = 1, . . . , c) is much larger when compared to the variance that appears within each group, then it is likely because the means aren't the same
\f\f
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


