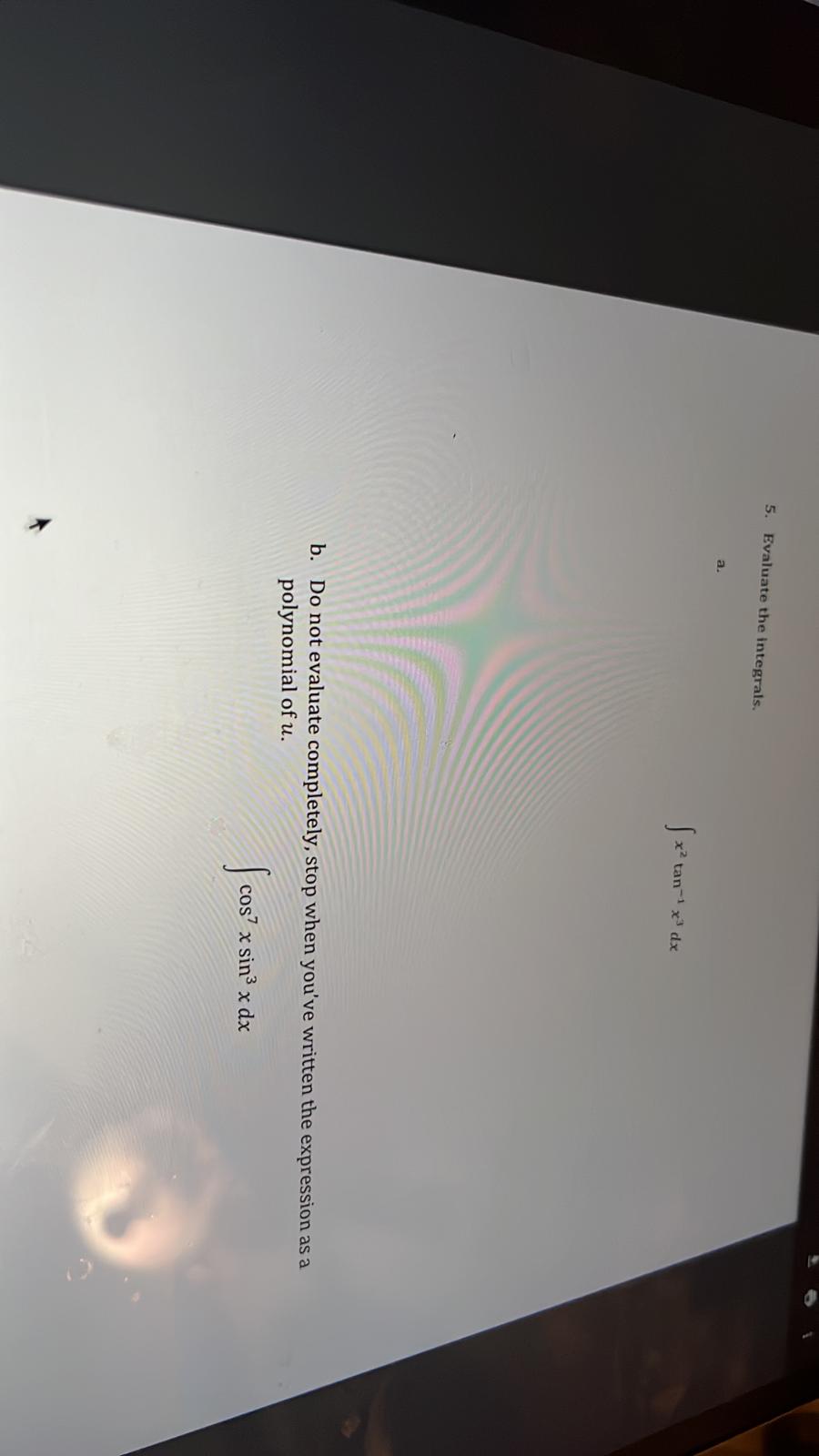
4. The equation for an ellipse centered at the origin is given by + = 1, the area of an ellipse can by found by first solving the above equation for y, yielding: y = 2 va2 - x2. Then the area can be found by integrating the function over the first quadrant and multiplying the result by 4. Do exactly that to find formula for area of an ellipse.5. Evaluate the integrals. *2 tan x dx b. Do not evaluate completely, stop when you've written the expression as a polynomial of u. cos x sin3 x dx6. Use one of the reduction formulas given at the end of the test to evaluate the following. tan5 x dx