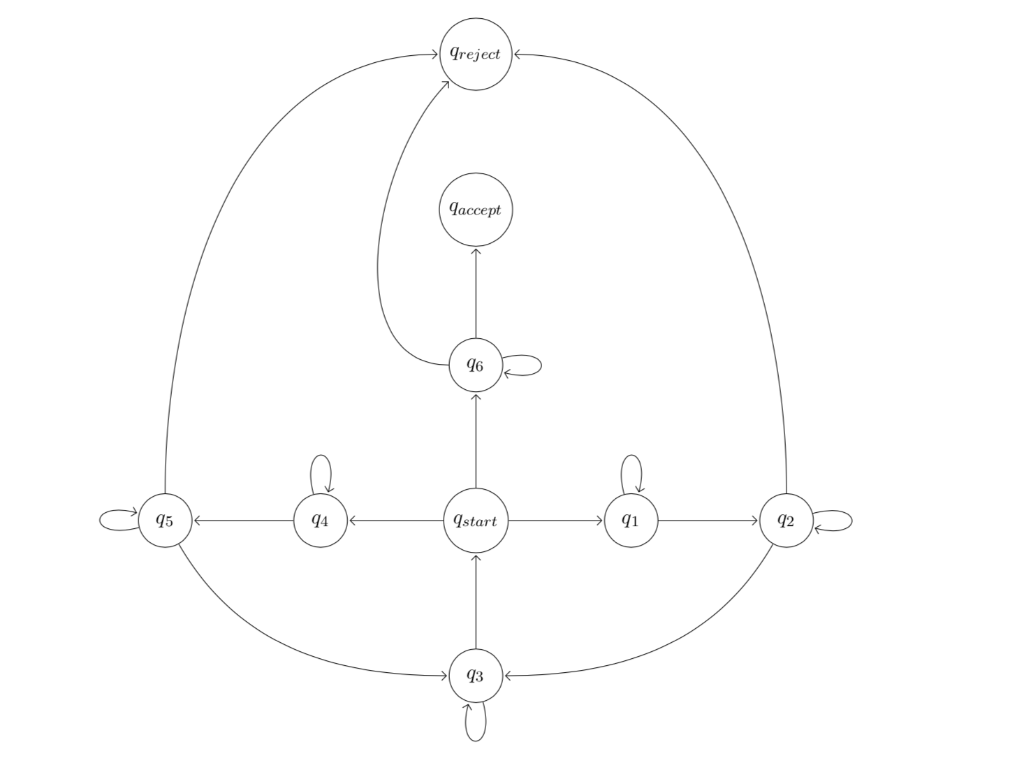
4. Turing Machines. Consider the language LBitwise-Complement = {a#ba, b {0,1}*, b = complement(a)} (e.g. if a = 010, then complement(a) = 101) whose members are comprised of two substrings that are the bitwise-complements of each other separated by a '#' character (e.g. 100#011" or 0#1, but not "1#10). Below is the state diagram for a Turing machine that decides this language, but its edges are missing state transitions. Complete the diagram by filling in the appropriate transitions of the form x + X', L/R where x, x' are symbols from the tape alphabet I = {0,1,#, 1}. Some edges may have more than one transition. You may assume that input string have been preprocessed and only inputs containing exactly one '#' character are now being considered. (Note: in order to type '#' in LATEX, you need to escape it with a backslash i.e., type '\#.) Preject qaccept 46 95 ) 94 Istart 91 92 93 4. Turing Machines. Consider the language LBitwise-Complement = {a#ba, b {0,1}*, b = complement(a)} (e.g. if a = 010, then complement(a) = 101) whose members are comprised of two substrings that are the bitwise-complements of each other separated by a '#' character (e.g. 100#011" or 0#1, but not "1#10). Below is the state diagram for a Turing machine that decides this language, but its edges are missing state transitions. Complete the diagram by filling in the appropriate transitions of the form x + X', L/R where x, x' are symbols from the tape alphabet I = {0,1,#, 1}. Some edges may have more than one transition. You may assume that input string have been preprocessed and only inputs containing exactly one '#' character are now being considered. (Note: in order to type '#' in LATEX, you need to escape it with a backslash i.e., type '\#.) Preject qaccept 46 95 ) 94 Istart 91 92 93