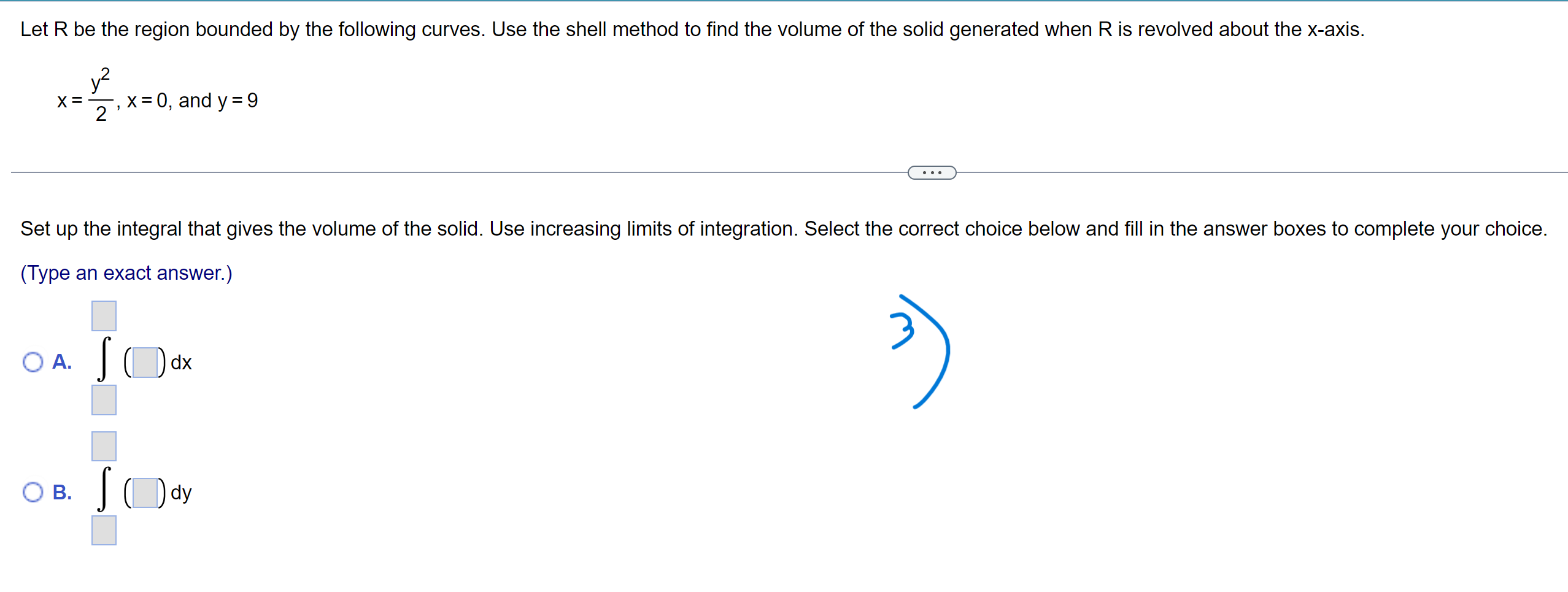
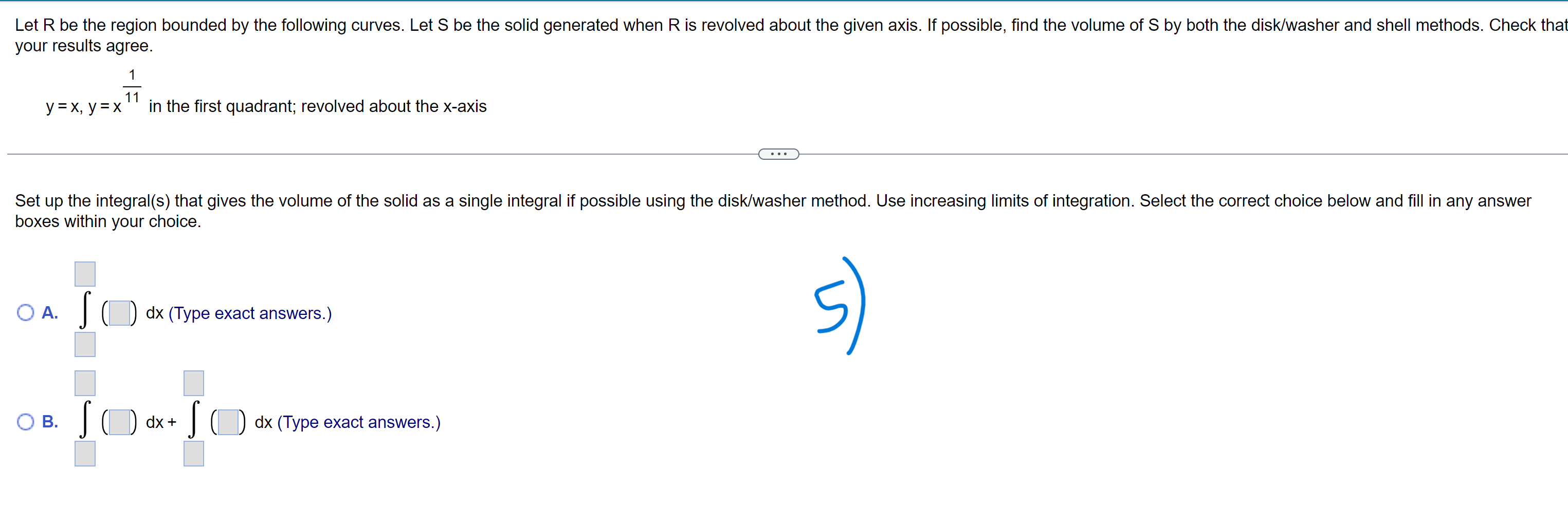
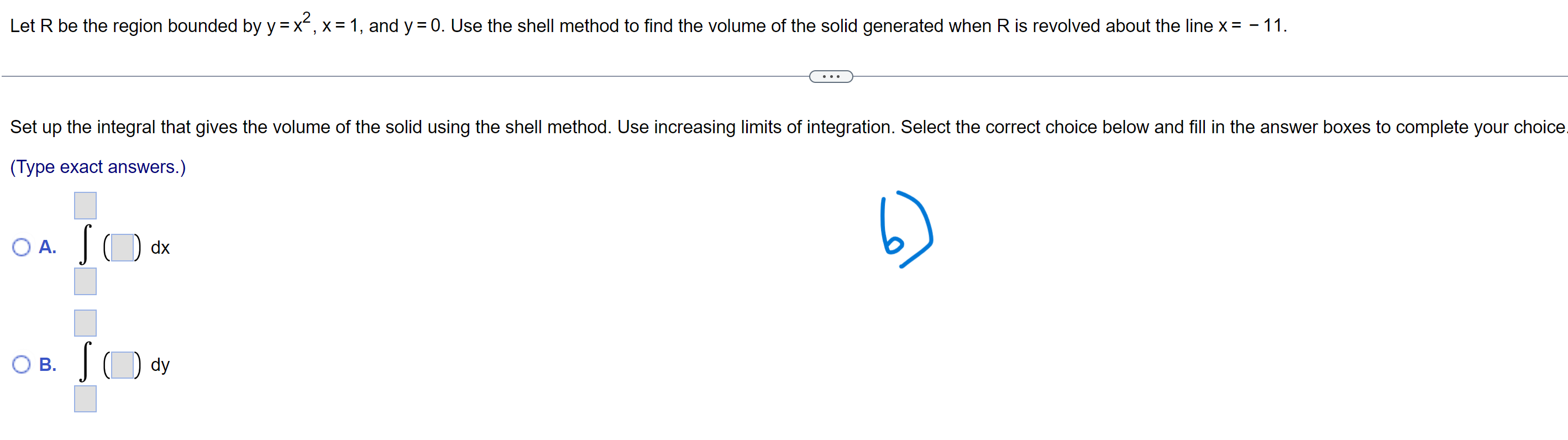
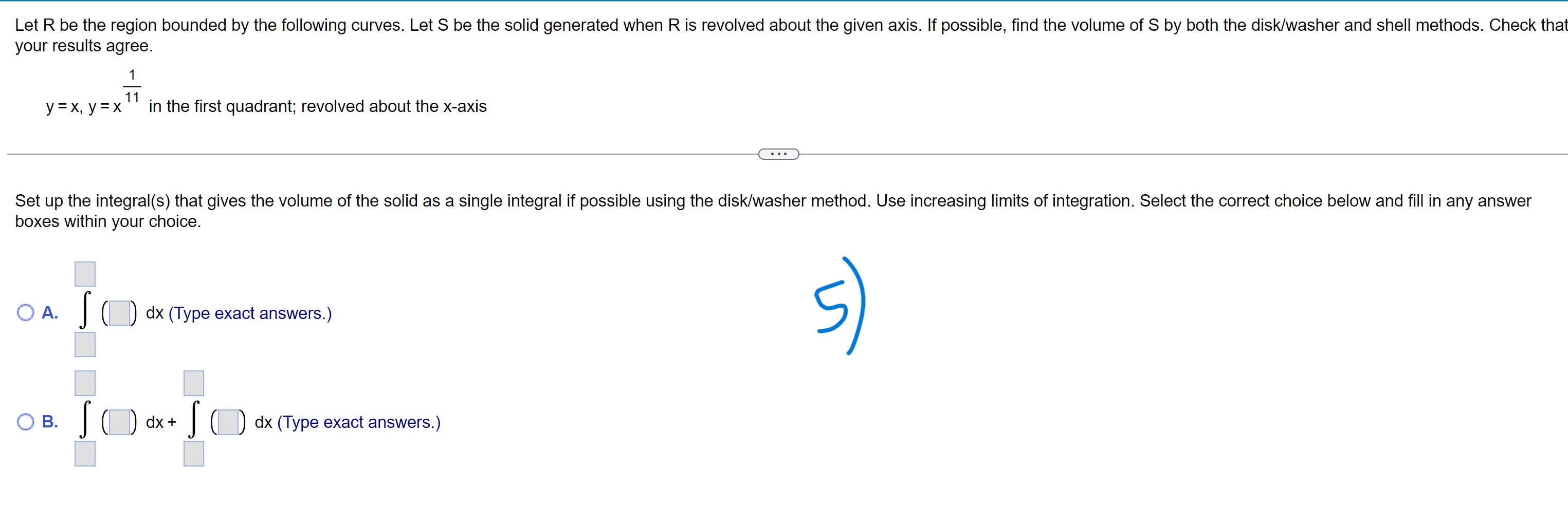
4 x 1 Let f(x) = + 2 and let R be the region bounded by the graph of f and the xaxis on the B 16x 2 interval [1, 3]. a. Find the area of the surface generated when the graph of f on [1, 3] is revolved about the X-axis. Use technology to evaluate or approximate the integral. b. Find the length of the curve y=f(x) on [1, 3]. c. Find the volume of the solid generated when R is revolved about the y-axis. d. Find the volume of the solid generated when R is revolved about the xaxis. Use technology to evaluate or approximate the integral. E) a. The area of the surface generated is . (Do not round until the final answer. Then round to the nearest tenth as needed.) A 1.5-mm layer of paint is applied to one side of the following surface. Find the approximate volume of paint needed. Assume that x and y are measured in meters. The spherical zone generated when the curve y = 1/ 18X x2 on the interval 1 SX S 6 is revolved about the X-axis. 7:) The volume of paint needed is m3. (Type an exact answer, using It as needed.) Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about the x-axis. 2 X=7, x=0,andy=9 Set up the integral that gives the volume of the solid. Use increasing limits of integration. Select the correct choice below and fill in the answer boxes to complete your choice. (Type an exact answer.) (:3 A. I( )dx 3 [1:3 B. J( )dy Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about the X-axis. 7t 1t y= sin1x,y=j;,y=/:,andx=0 Set up the integral that gives the volume of the solid. Use increasing limits of integration. Select the correct choice below and fill in the answer boxes to complete your choice. (Type an exact answer.) C? A. I dx LY Let R be the region bounded by the following curves, Let S be the solid generated when R is revolved about the given axis' If possible, find the volume of S by both the disk/washer and shell methods, Check that your results agree. 1 y = x, y = x11 in the first quadrant; revolved about the x-axis Set up the integral(s) that gives the volume of the solid as a single integral if possible using the disk/washer method. Use increasing limits of integration, Select the correct choice below and fill in any answer boxes within your choice. '1:- A. I ( J dx (Type exact answers.) S Li B. I ( ) dx+ I ( ) dx (Type exact answers.) 2 Let R be the region bounded by y = X ,x = 1, and y = 0. Use the shell method to nd the volume of the solid generated when R is revolved about the line x = -11. Set up the integral that gives the volume of the solid using the shell method. Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice (Type exact answers.) a A. j r ) dx L Use both the washer method and the shell method to find the volume of the solid that is generated when the region in the first quadrant bounded by y = x2, y = 9, and x = 0 is revolved about the line y = 3. E) Set up the integral that gives the volume of the solid as a single integral if possible using the disk/washer method. Select the correct choice below and fill in any answer boxes within your choice. (Type exact answers.) C::- A. I( )dx 9' v:::- B. I( My A torus is formed when a circle of radius 3 centered at (4,0) is revolved about the y-axis YT a. Use the shell method to write an integral for the volume of the torus. b. Use the washer method to write an integral for the volume of the torus, 4 - 3 ' c. Find the volume of the torus by evaluating one of the two integrals obtained in parts (a) and (b). (Hint: Both integrals can be evaluated without using the Fundamental ' Theorem of Calculus.)