Question: 4.10 CNF vs. DNE. A Boolean formula is in disjunctive normal form (DNF) if it is an on of clauses, each of which is the

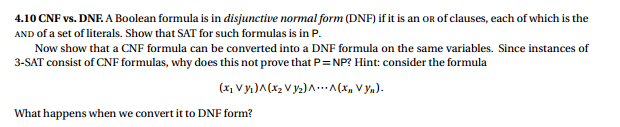
4.10 CNF vs. DNE. A Boolean formula is in disjunctive normal form (DNF) if it is an on of clauses, each of which is the AND of a set of literals. Show that SAT for such formulas is in P. Now show that a CNF formula can be converted into a DNF formula on the same variables. Since instances of 3-SAT consist of CNF formulas, why does this not prove that P = NP? Hint: consider the formula What happens when we convert it to DNF form

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The SAT problem introduced in the class is the CNF Satisfiability Problem ( CNF - SAT ) , one version of the Satisfiability Problem. In CNF - SAT, the Boolean formula is specified in the Conjunctive...

Module 04 Written Assignment 1. Write Disjunctive Normal Form (DNF) and Conjunctive Normal Form (CNF) corresponding to the following truth table: p T T T T F F F F q T T F F T T F F r Truth Value T T...

Shorter expression illustrated as syntax trees and logic diagrams - Computer Processors Need help with question 5 Please answer correctly for thumbs up For each of the following boolean formula...

K-maps - Computer Processors Need help with question 4 Please answer correctly for thumbs up For each of the following boolean formula construct a truth table (T, and false respectively) 1. denote...

Circuit diagram and K-map question Please can someone help me answer the k-map part of the question to minimise the expression and drawing the circuit diagrams for them? Will leave thumbs up if all...

True / False with explexplanation ( 1 ) By converting a formula that is in disjunctive normal form into a formula in conjunctive normal form, the formula can become exponentially larger. ( 2 ) The...

In this problem, we will give another proof that the set of connectives {-, A, V} is adequate for propositional (Boolean logic.) To do this, we will show that every n-ary Boolean operator (n > 1)...

1 CNF and DNF Formulas In the case of the following formulas point out whether they are CNF or DNF formula writing " CNF " or " DNF " if necessary: [ ( p v v n o t q ) ? ? ( n o t p v v n o t q v v r...

1 C N F and DNF Formulas In the case of the following formulas point out whether they are CNF or DNF formula writing " CNF " or " DNF " if necessary: [ ( p v v n o t q ) ? ? ( n o t p v v n o t q v v...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Prepare a line graph of these data. Do the data appear to be stationary or nonstationary? Discuss in detail.

Using the concept of TVM, you can calculate the amount I need to save each year to reach my retirement savings goal. Information: 1. Current Age: 30 2. Desired Retirement Age: 65 3. Annual Salary:...

Please provide the answer to this general accounting question using the right approach. The Green Valley Company has provided the following information after year-end adjustments: - The allowance for...

The following information pertains to the October operating budget for Flockhart Corporation . Budgeted sales for October $100,000 and November $200,000 Collections for sales are 60% in the month of...