4.2 Homework - The Mean Value Theorem (Homework)

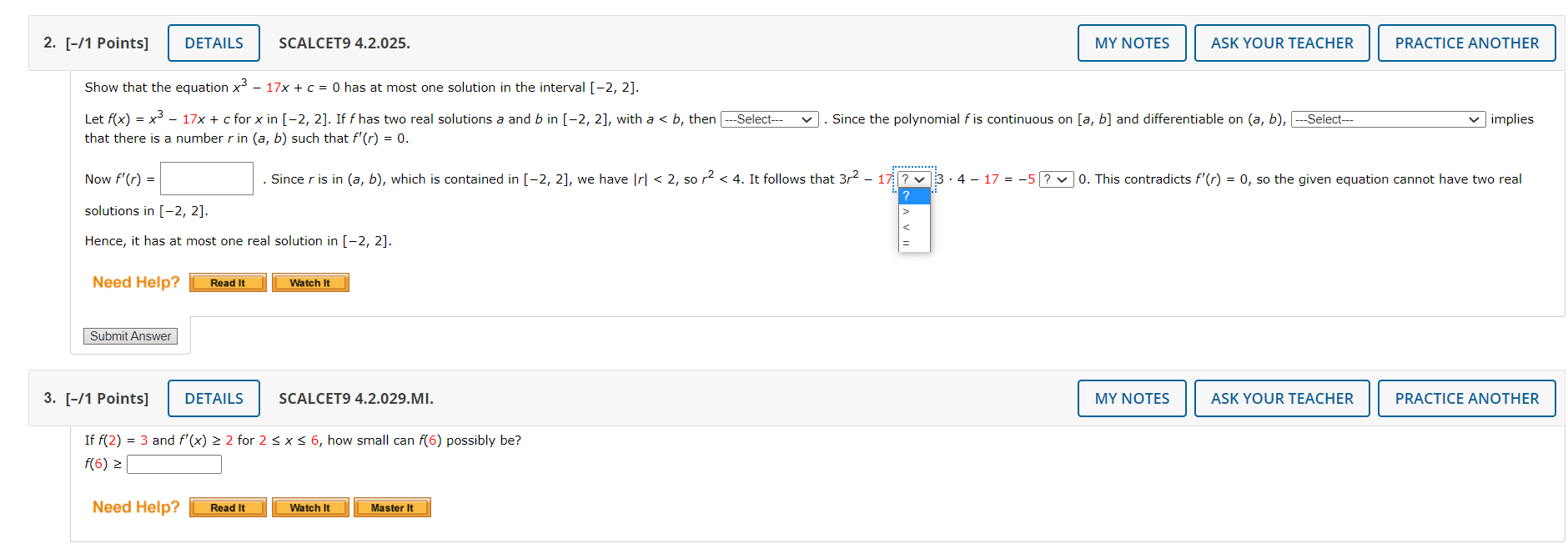
1. [-/1 Points] DETAILS SCALCET9 4.2.016.EP. MY NOTES ASK YOUR TEACHER Consider the following function and closed interval. f(x) = x5 - 3x + 9, [-2, 2] Is f continuous on the closed interval [-2, 2]? Yes, it does not matter if f is continuous or differentiable; every function satisfies the mean value theorem. O Yes, fis continuous on [-2, 2] and differentiable on (-2, 2) since polynomials are continuous and differentiable on R. O No, f is not continuous on [-2, 2]. O No, fis continuous on [-2, 2] but not differentiable on (-2, 2). O There is not enough information to verify if this function satisfies the mean value theorem. If fis differentiable on the open interval (-2, 2), find f'(x). (If it is not differentiable on the open interval, enter DNE.) f' ( x ) = Find f(-2) and f(2). (If an answer does not exist, enter DNE.) F( - 2 ) = f( 2 ) = Find f(b) - f(@ for [a, b] = [-2, 2]. (If an answer does not exist, enter DNE.) b - a f(b ) - f(@) = b - a Determine whether the mean value theorem can be applied to f on the closed interval [-2, 2]. (Select all that apply.) O Yes, the Mean Value Theorem can be applied. No, because f is not continuous on the closed interval [-2, 2]. O No, because f is not differentiable on the open interval (-2, 2). No, because _(D) - 2 is not defined. b - a If the mean value theorem can be applied, find all values of c that satisfy the conclusion of the mean value theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE). C =2. [-/1 Points] DETAILS SCALCET9 4.2.025. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Show that the equation x" - 17x + c = 0 has at most one solution in the interval [-2, 2]. Let f(x) = x3 - 17x + c for x in [-2, 2]. If f has two real solutions a and b in [-2, 2], with a I A Hence, it has at most one real solution in [-2, 2]. Need Help? Read It Watch It Submit Answer 3. [-/1 Points] DETAILS SCALCET9 4.2.029.MI. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER If f(2) = 3 and f'(x) 2 2 for 2