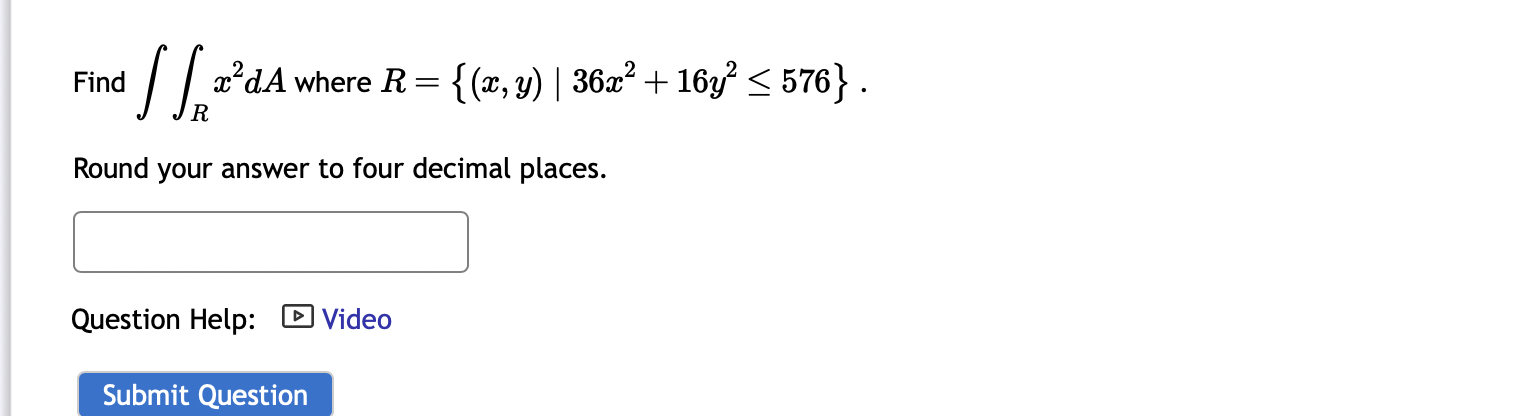
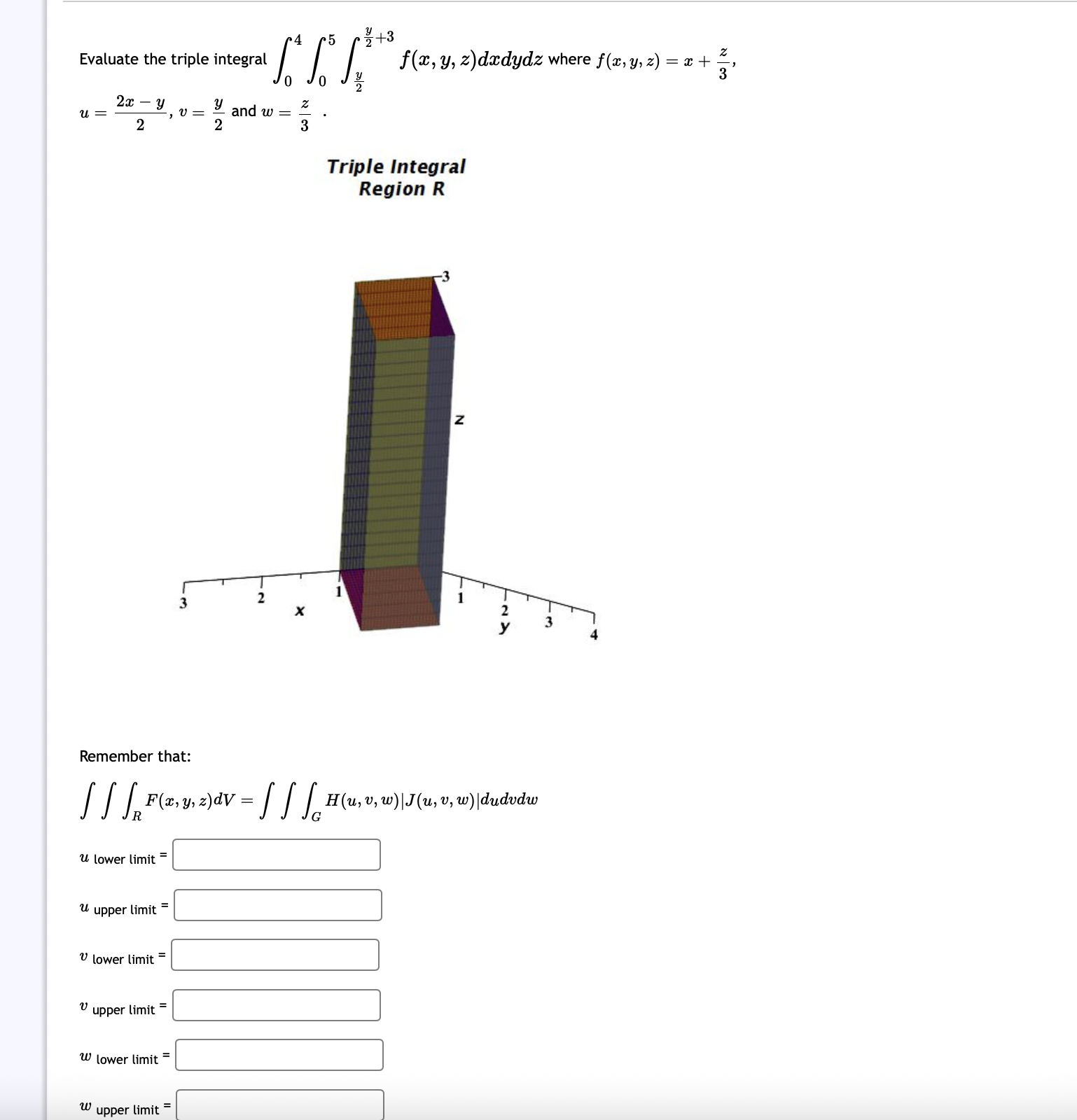
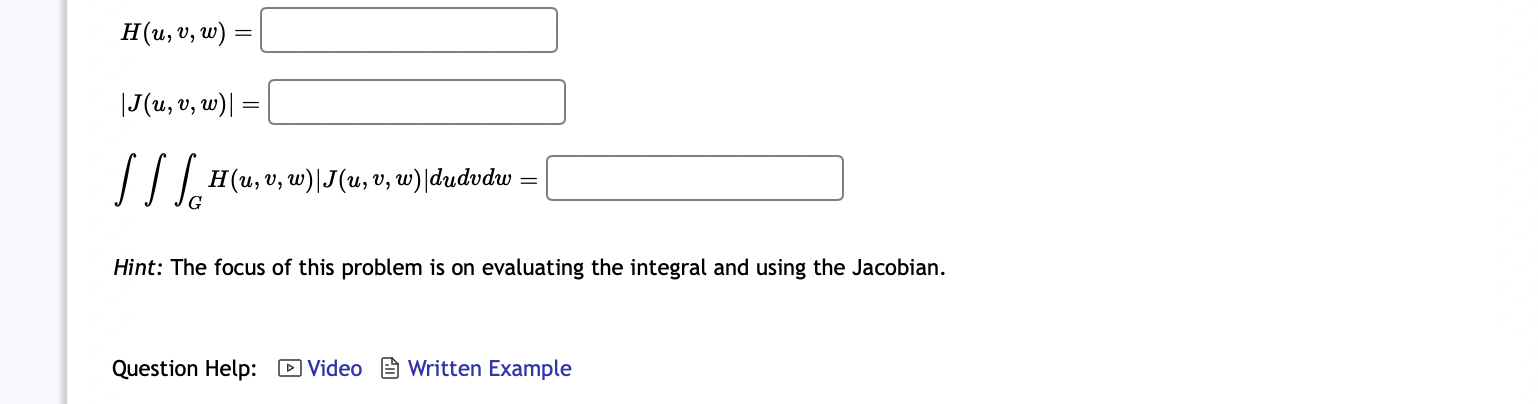
4x - 4y SSR -3x - 5y R 4x - 4y = 0, 4x - 4y = 2, 3x - 5y = 1, 3x - 5y = 9. Round your answer to 4 decimal places. Find dA, where R is the parallelogram enclosed by the lines Question Help: Video Submit Question In order to find the area of an ellipse, we may make use of the idea of transformations and our knowledge of 2 (x-1)2 (y+4) the area of a circle. For example, consider R, the region bounded by the ellipse = 1. 16 4 The easiest transformation to choose makes U = which should be easily inverted to obtain x = leading to a Jacobian of and v= a(x, y) d(u, v) And since and y = + y) A= ,0 (1, 0) dA d(u, v) S calculate the area by multiplying the area and the Jacobian, arriving at (give an exact answer) dudu where the transformed region S is bounded by u + = 1, we 1 R Round your answer to four decimal places. Find xdA where R Question Help: Video Submit Question = {(x, y) | 36x + 16y 576} . Let D be an ellipse rotated counterclockwise by radians, as pictured below. Before rotation, the horizontal 3 radius was 5 and vertical radius was 6. -7 -6 -5 -4 -3 -2 -1 Convert 2T 1 6 6 7+ 6 5 4 3 2 1 -2 -3 -4 1 2 3 4 5 16 -2x + 4y)dA into an integral over a polar integral over a unit circle. (type theta for 8) D dr de Evaluate the triple integral U = 2x - Y 2 u lower limit U upper limit v lower limit= v upper limit= 3 2 w lower limit= V= upper limit= 3 and w= 2 2 4 5 L S L Z 3 Remember that: [ ] [ F(x, y, z)dv = [ ] [ H(u, v, w)|J (u, v, w)|dudvdw R G X 2/2+3 . f(x, y, z)dxdydz where f(x, y, z) Triple Integral Region R Z 2 = x + 22/02 Z H(u, v, w) = |J(u, v, w)| = = [ ] [ H(u, v, w)|J(u, v, w)|dudvdw : G Hint: The focus of this problem is on evaluating the integral and using the Jacobian. Question Help: Video Written Example