Question: 5. (09.01 HC) For the parametric curve defined by x(t) = 2cos2t, y(t) = 2sin2t. Part A: For the given parametric curve, determine where )
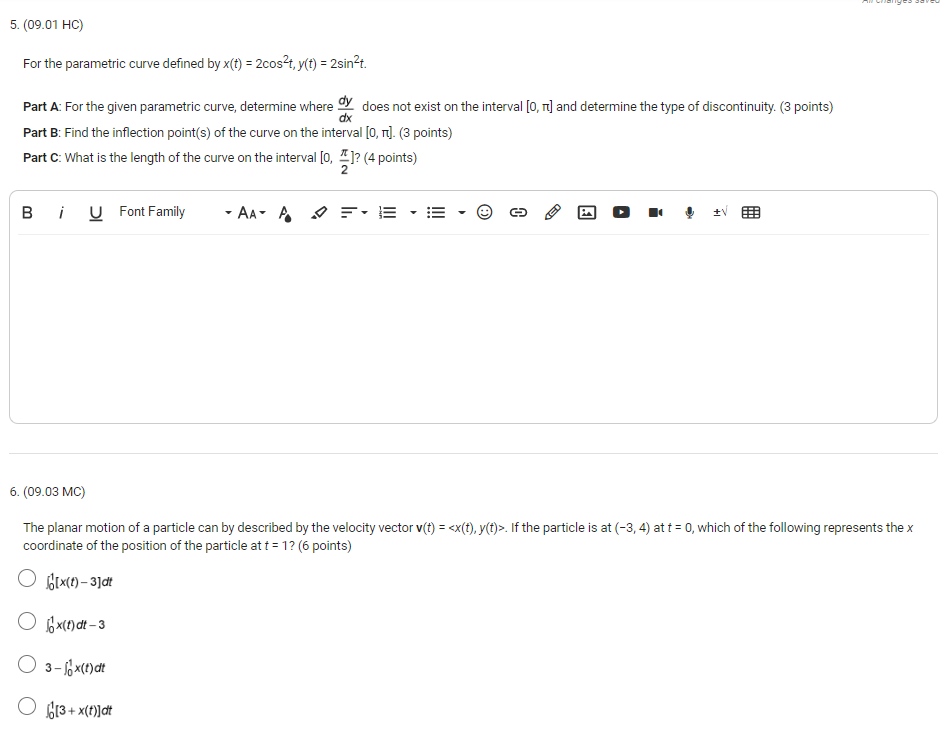
![where ) does not exist on the interval [0, ] and determine](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666806b7a891a_495666806b791e5d.jpg)
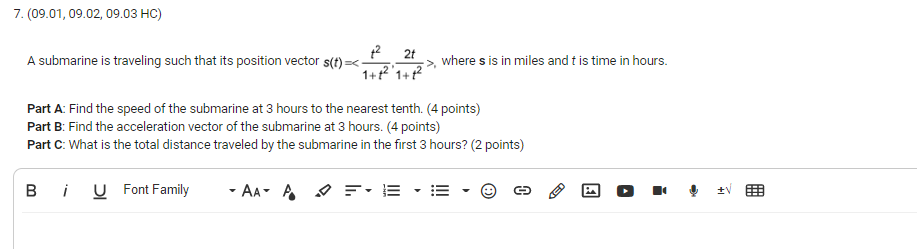
5. (09.01 HC) For the parametric curve defined by x(t) = 2cos2t, y(t) = 2sin2t. Part A: For the given parametric curve, determine where ) does not exist on the interval [0, ] and determine the type of discontinuity. (3 points) dx Part B: Find the inflection point(s) of the curve on the interval [0, ]. (3 points) Part C: What is the length of the curve on the interval [0, #]? (4 points) B i U Font Family AAT A DE . E . E . 3 9 0 6. (09.03 MC) The planar motion of a particle can by described by the velocity vector v(t) =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


