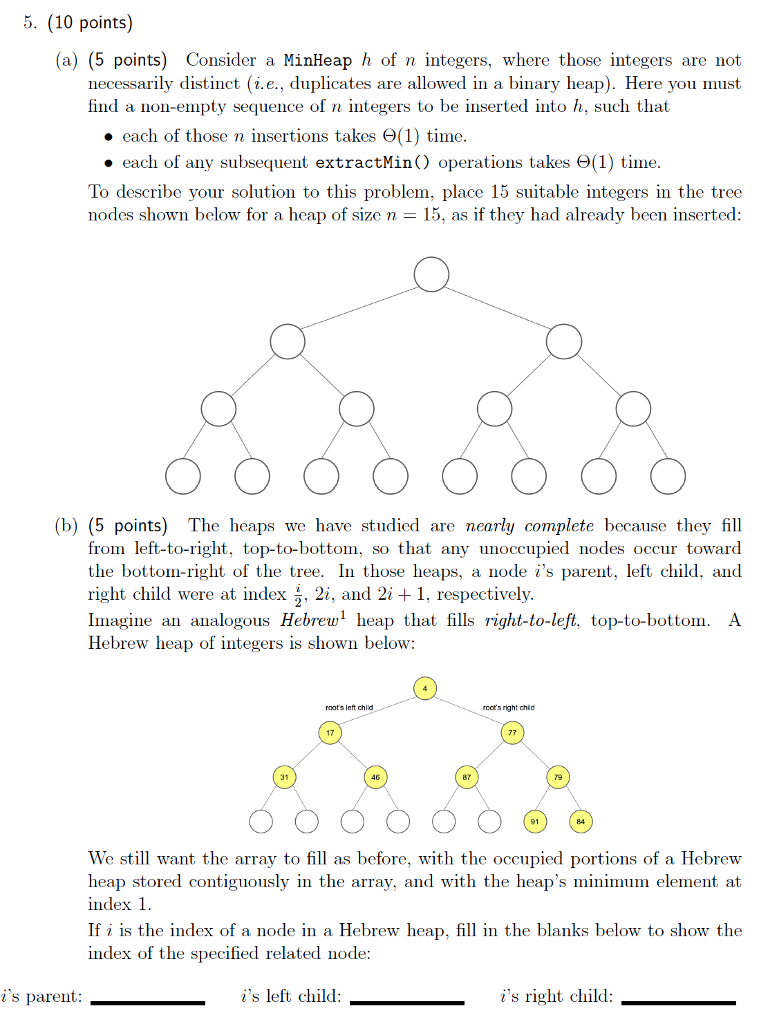
5. (10 points) (a) (5 points) Consider a MinHeap h of n integers, where those integers are not necessarily distinct (i.e., duplicates are allowed in a binary heap). Here you must find a non-empty sequence of n integers to be inserted into h, such that . each of those n insertions takes (1) time . each of any subsequent extractMin() operations takes (1) time. To describe your solution to this problem, place 15 suitable integers in the tree nodes shown below for a heap of size n = 15, as if they had already been inserted (b) (5 points) The heaps we have studied are nearly complete because they fill from left-to-right, top-to-bottom, so that any unoccupied nodes occur toward the bottom-right of the tree. In those heaps, a node i's parent, left child, and right child were at index 2, and 2i + 1, respectively Imagine an analogous Hebrew heap that fills right-to-left, top-to-bottom. A Hebrew heap of integers is shown below: cots right chi 17 31 46 87 79 91 We still want the array to fill as before, with the occupied portions of a Hebrew heap stored contiguously in the array, and with the heap's minimum element at index 1 If i is the index of a node in a Hebrew heap, fill in the blanks below to show the index of the specified related node i's parent i's left child i's right child