Question: 5. (10 points) Let Sn = EX. (n21) i=1 be a random walk on R where X1, X2, . .. is a sequence of i.i.d.

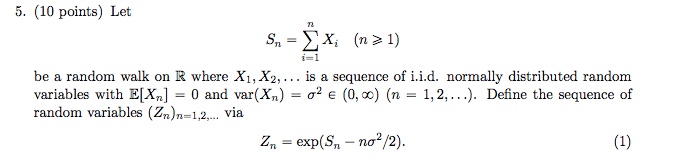
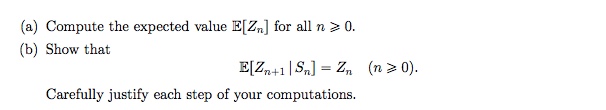
5. (10 points) Let Sn = EX. (n21) i=1 be a random walk on R where X1, X2, . .. is a sequence of i.i.d. normally distributed random variables with E[X,] = 0 and var(X, ) = o' e (0, co) (n = 1, 2,...). Define the sequence of random variables (Zn)n=1,2,... via Zn = exp(Sn - no?/2). (1)(a) Compute the expected value E[Z,] for all n 2 0. (b) Show that E[Zn+1 |S,] = Zn (n20). Carefully justify each step of your computations

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Which of two widely prescribed drugsLipitor or Pravacholhelps lower bad cholesterol more? In an experiment, called the PROVE-IT Study, researchers recruited about 4000 people with heart disease as...

4. (10 points) Let Sn = So + > Xi (n2 1) i= 1 where X1; X2, ... is a sequence of i.i.d. random variables independent of the random variable So such that P[X/ = +1] = P[X = =1] = (1 =1). (a) Compute...

Question: A company is named with your last name (e.g. Miao). It has a finance department which requires a service to be high available. You will need to 1) complete the requirement analysis (with...

ANSWER ALL QUESTIONS. BE SURE TO ANSWER 7.1.8. A balanced die is rolled 3 times. Let x1 be the number of times 1 appears and x2 be the number of times 2 appears. Work out the joint probability...

Problem 1. Problem 2. Problem 3. Problem 4. 1. (10 points) Let X; for i =1,2,..., n be independent and identically distributed random variables with mean u > 0 and standard deviation o > 0. When we...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

4. (10 points) Let X1, X2, X3, ... be a sequence of independent random variables, where X; is exponentially distributed with parameter 1 for all i 2 1. We define Sn = EXi for all n > 1. i=1 (a) Does...

Q.2 Answer the following questions. (14 marks) a. Given {Nn)n21 number of successes in a Bernoulli stochastic process. Compute and P{N1 = a, N3 = b, N4 = c}, where choose a, b, c E Zt. b. Compute...

(10 points) Let X1, X2,... be a sequence of independent random variables with identical dis- tribution. Let their mean be given by E(X;) = / and their variance by V(X;) = o'. Moreover, define Sn =...

10 points) Let X1; X2, X3, ... be a sequence of independent random variables, where X; is exponentially distributed with parameter 1 for all i 2 1. We define Sn = Xi for all n 2 1. i=1 (a) Does the...

Nearly all companies confront loss contingencies of various forms. Required: a. Describe what conditions must be met for a loss contingency to be accrued with a charge to income. b. Explain when...

In the current year, Jeanette, an individual in the 25% marginal tax bracket, recognized a $20,000 long-term capital gain. Also in the current year, Parrot Corporation, a C corporation in the 25%...

El ensayo es un g nero literario enlazado solamente a las circunstancias del presente. True False

Exercise 10-2 (Part Level Submission) on May 15, Criqui Outback Clothiers borrowed some money on a 4-month note to provide cash during the slow season of the year. The interest rate on the note was...