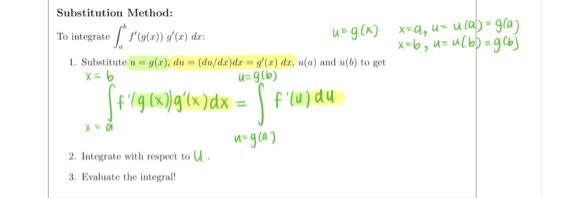
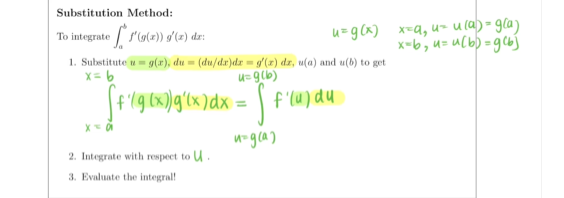
5. (10 pts) Consider the indefinite integral I = csc2(@) cot(0)de. (a) (5 pts) Evaluate I using the Substitution Method with u = cot(0). (b) (5 pts) Evaluate I using the Substitution Method with a different choice of u.The Substitution Rule in Indefinite Integrals If u = p(x) is a differentiable function whose range is an interval I, and f is continuous on /, then [f ' ( u) du = flu)+ c du = g'(x ) dx = f(g (x ) )+C we propose S f /gum ) g' (x ) dx = fig ( * ) )+ c d dx ( f ( g ( x ) ) + c) = = ( fig (x) ) = [f' (9 (x)) . g'(x) we accomplish the transformation above by using of variablesSubstitution Method: To integrate [fatz)) s'(z) dr: u=g (x) *=q, u= ula)= glay x=b, u= u[b) = g(6] 1. Substitute a = g(x), du = (du/de)da = g'(x) dx, u(a) and u(b) to get X= b u= g(b) [f '19 (x)g'(x) dx= f' lu ) du u= g (a ] 2. Integrate with respect to U . 3. Evaluate the integral