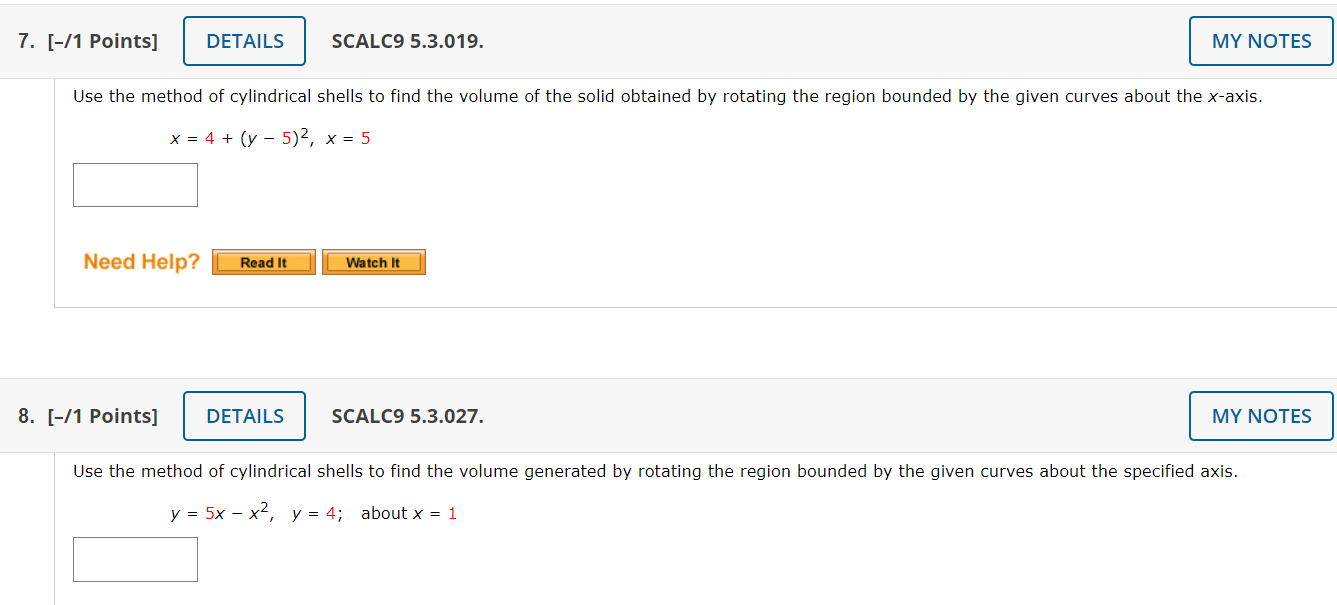
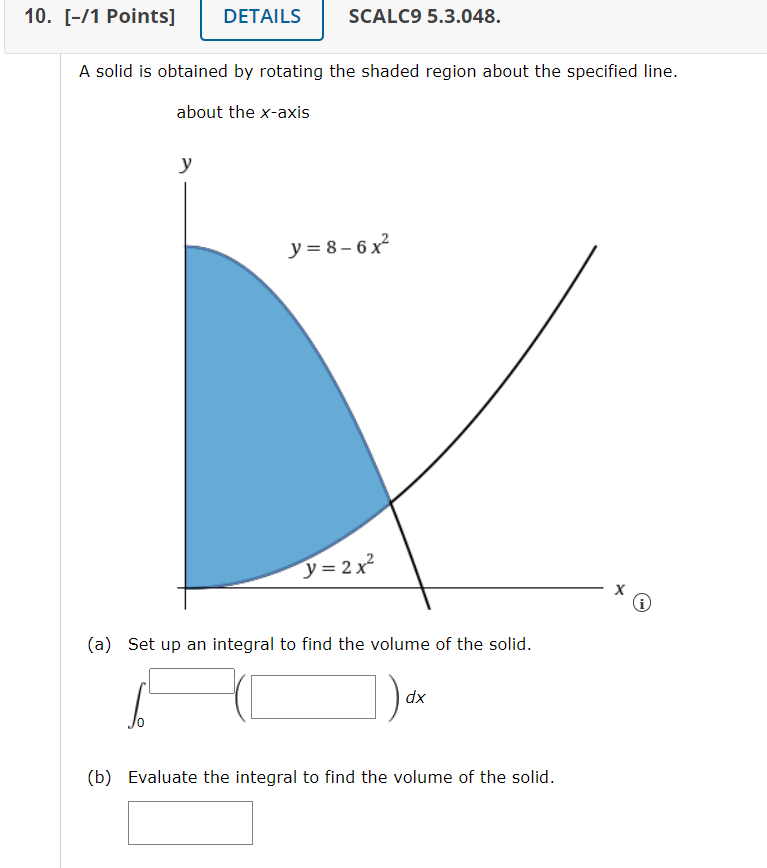
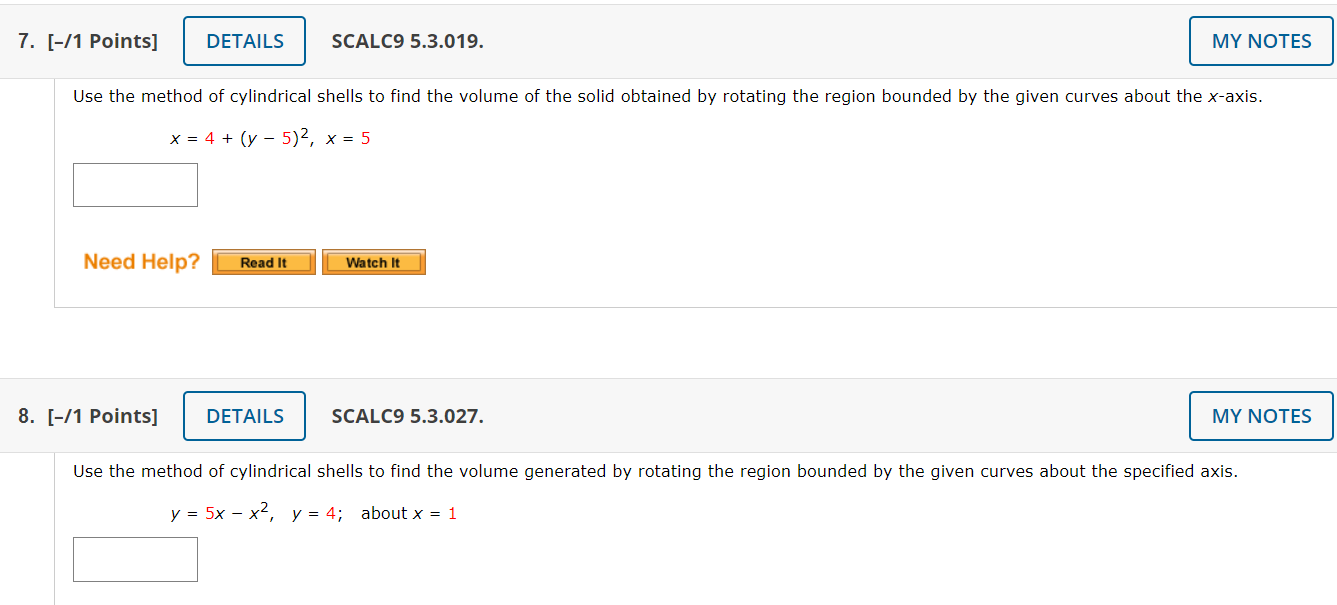
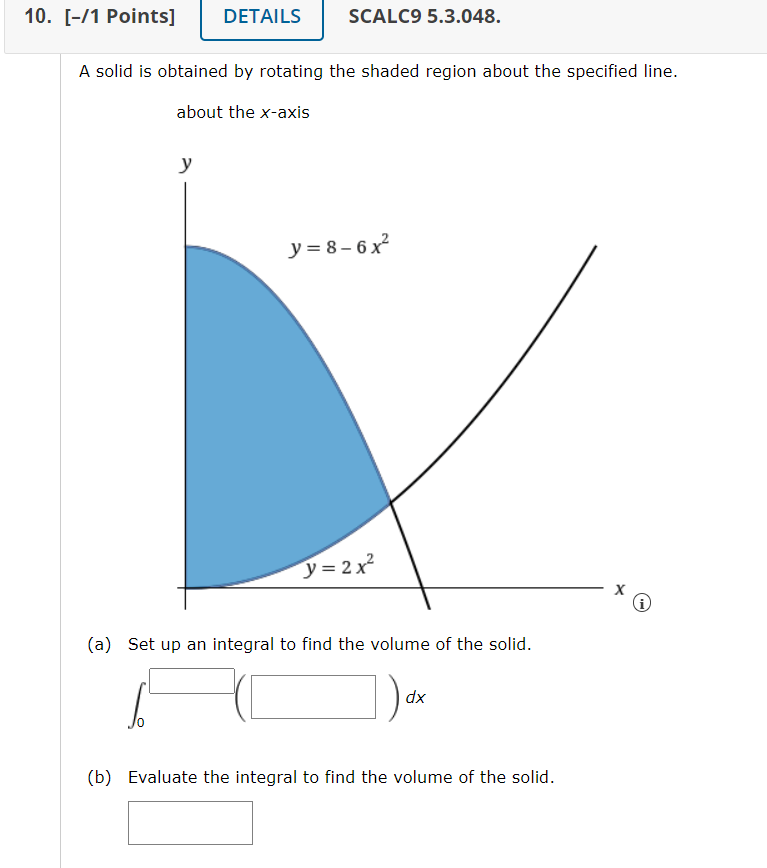
5. [11 Points] ' DETAILS l SCALES 5.3.050. u solid is obtained bv rotating the shaded region about the specified line. about the yaxis J" ()a Set up an integral to find the volume of the solid. [q- )dx (b) Evaluate the integral to find the volume of the solid. 7. [-/1 Points] DETAILS SCALC9 5.3.019. MY NOTES Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = 4+ (y - 5)2, x = 5 Need Help? Read It Watch It 8. [-/1 Points] DETAILS SCALC9 5.3.027. MY NOTES Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = 5x - x4, y = 4; about x = 19. [11 Points] DETAILS SCALCB 5.3.028. MY NOTES Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Y=\\/, x=4y; aboutx=l7 1U. [I1Puints] l DETAILS l SCALES 5.3.048. A solid is obtained by rotating the shaded region about the specified line. about the Xaxis J' {a} Set up an integral to find the volume of the solid. 1:( ) w o (b) Evaluate the integral to find the volume of the solid