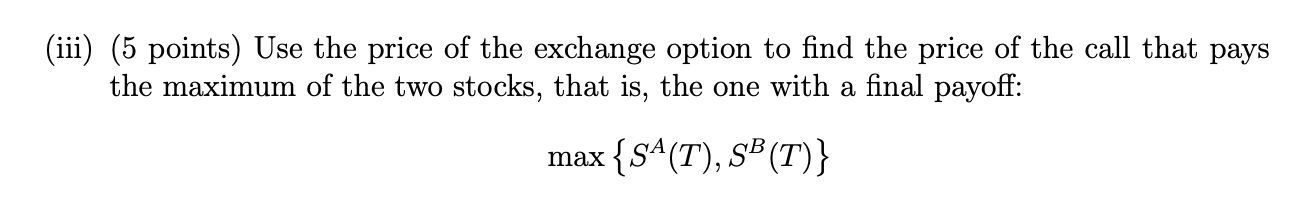
5 (30 points) Long Question 4 This question is more difficult compared to other questions. The purpose here is to test whether you understand the logic/intuition of option pricing or just merely memorize the formulas in lecture notes. The exchange option is a contract that gives the holder the right to exchange asset B for asset A. Hence the payoff of the European exchange call option can be written as Cexchange = max {0, SA(T) SB(T)} SA(T) = SB(T) max {0, SB(T) { -1} The way to price these exchange options is by modeling the dynamics of the ratio of the two prices instead of the dynamics of each stock price. For example, consider a 1-period binomial tree. The initial ratio is given by SA SB Next period the ratio can go up to ux or down to dx Let the data of this one-period tree be given by SA = 100 So = 125 u= 2 d=0.5 Assume no dividend payments for stock A or B. (i) (20 points) Compute a replicating portfolio for the 1-period European exchange call option that invests in stock A and stock B. How many shares of stock A and stock B do you want to buy? Use this replicating portfolio to determine the price of the call. (HINT: No need to use bonds.) (ii) (5 points) Price the American exchange call (which can be exercised immediately). (iii) (5 points) Use the price of the exchange option to find the price of the call that pays the maximum of the two stocks, that is, the one with a final payoff: max {SA(T), SB(T)} 5 (30 points) Long Question 4 This question is more difficult compared to other questions. The purpose here is to test whether you understand the logic/intuition of option pricing or just merely memorize the formulas in lecture notes. The exchange option is a contract that gives the holder the right to exchange asset B for asset A. Hence the payoff of the European exchange call option can be written as Cexchange = max {0, SA(T) SB(T)} SA(T) = SB(T) max {0, SB(T) { -1} The way to price these exchange options is by modeling the dynamics of the ratio of the two prices instead of the dynamics of each stock price. For example, consider a 1-period binomial tree. The initial ratio is given by SA SB Next period the ratio can go up to ux or down to dx Let the data of this one-period tree be given by SA = 100 So = 125 u= 2 d=0.5 Assume no dividend payments for stock A or B. (i) (20 points) Compute a replicating portfolio for the 1-period European exchange call option that invests in stock A and stock B. How many shares of stock A and stock B do you want to buy? Use this replicating portfolio to determine the price of the call. (HINT: No need to use bonds.) (ii) (5 points) Price the American exchange call (which can be exercised immediately). (iii) (5 points) Use the price of the exchange option to find the price of the call that pays the maximum of the two stocks, that is, the one with a final payoff: max {SA(T), SB(T)}