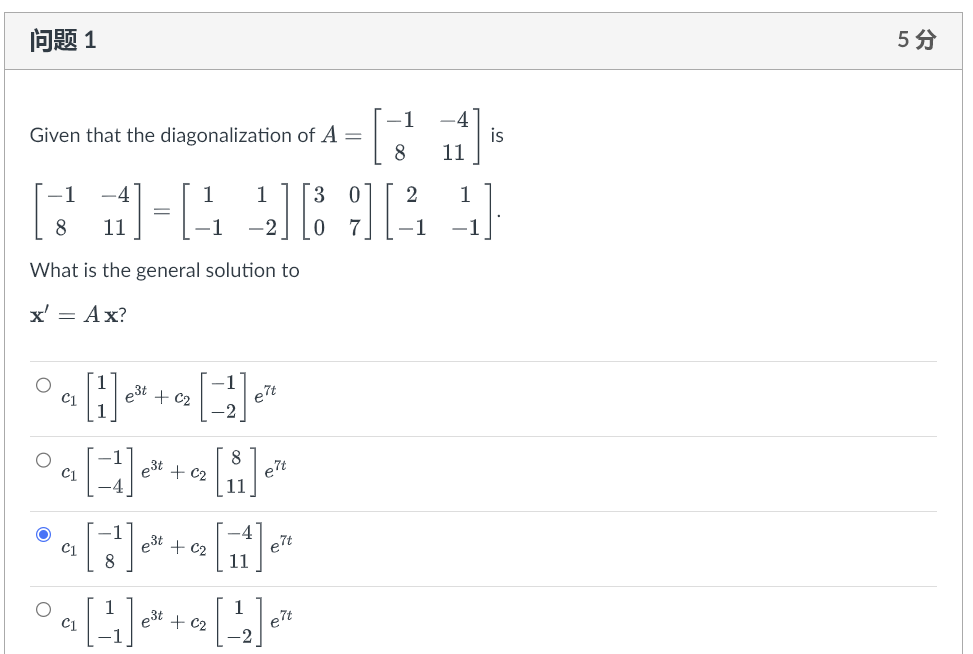
Question: 5 53 - : 1 1 4 Given that the diagonalization of A = is 8 11 8 11 What is the general solution to

![O CI 3t + C2 2] ert453 Eigenvalues of A are X1](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ee40e5de6_8486703ee40d7081.jpg)
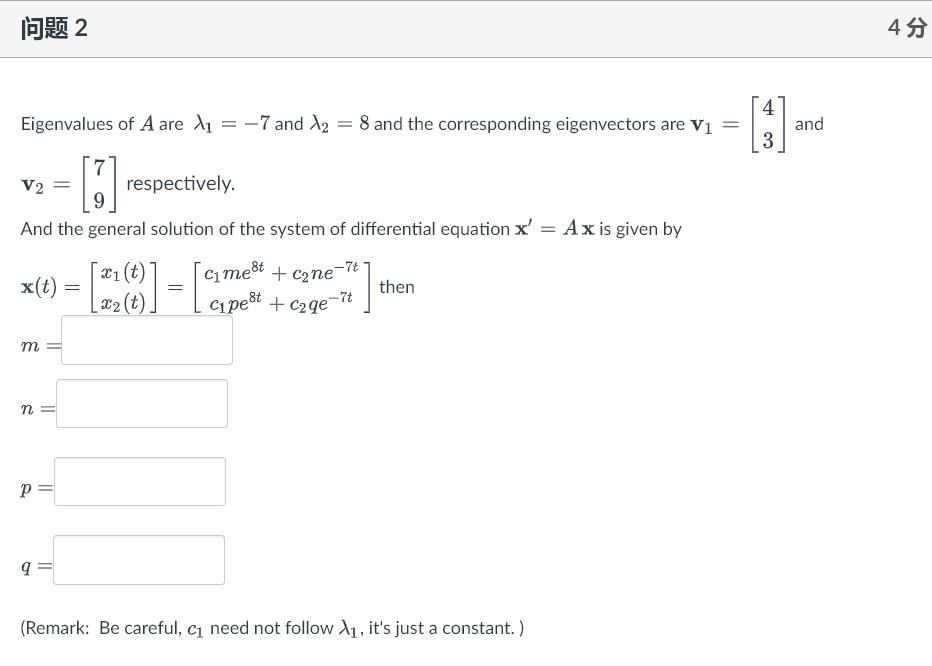
5 53 - : 1 1 4 Given that the diagonalization of A = is 8 11 8 11 What is the general solution to x' = Ax? O O O 7t C1 e' 11 O CI 3t + C2 2] ert453 Eigenvalues of A are X1 = -7 and 12 = 8 and the corresponding eigenvectors are V1 and 3 V 2 [. respectively. And the general solution of the system of differential equation x' = A x is given by cimet + cone-7t 7 x(t) = X1 (t) then *2 (t) Ci pest + cage-7t m P = (Remark: Be careful, c1 need not follow )1, it's just a constant. )J The matrix A = has eigenvalues X1 = 4 and 12 = 6 and 3 corresponding eigenvectors v1 = $ 1 and va = [1] Let x(t) be the position of a particle at time t . Suppose we solve system of differential equations x1 (t) x' (t) = x1(t) = A to obtain Lab( t). 2 2 (t ) *1 (0) 11 and then applying it to the initial condition x(0) = = then c1 2 2 (0) 23 and C210 Let A be a matrix whose eigenvalues are X1 = 3, 12 = 6 and corresponding eigenvectors are V1 = and V 2 = Let x(t) be the position of a particle at time t that satisfies the initial 34 value problem x' = Ax, x(0) = 18 C1 C2 m n
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


