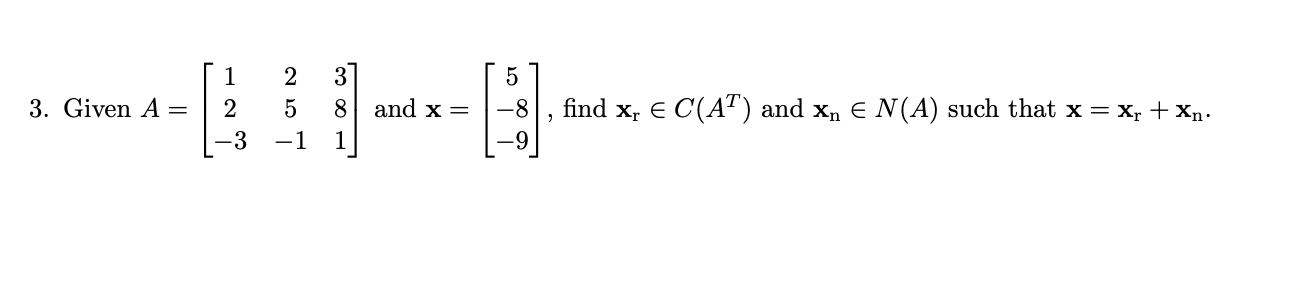
5. (a) Compute the projection matrices P, and P onto the lines through a; = (1, 1,1) and az = (-2, 1,1), respectively. Multiply P; and P and explain why their product P, P; is what it is. 1 2 (b) Find the orthogonal projection of b = (1, 2, 3) onto the column space of the matrix A= | 3 7 -2 -3 1 -2 (c) Find the orthogonal projection of b = (1, 1,2) onto the left null space of the matrix A= |3 4]|. 5 6 1 -1 3 6. (a) Let A=1|1 0 1]|. 0 1 -2 (i) Find the projection matrix onto the column space C(A). (i) What vector in C(A) is closest to b = (3,3, 6)? (b) For a vector b =(2,1,2) and a plane P: 3z 2y 4z =0 (i) Compute a basis of P. (i) Compute the projection of vector b onto the plane P. \f