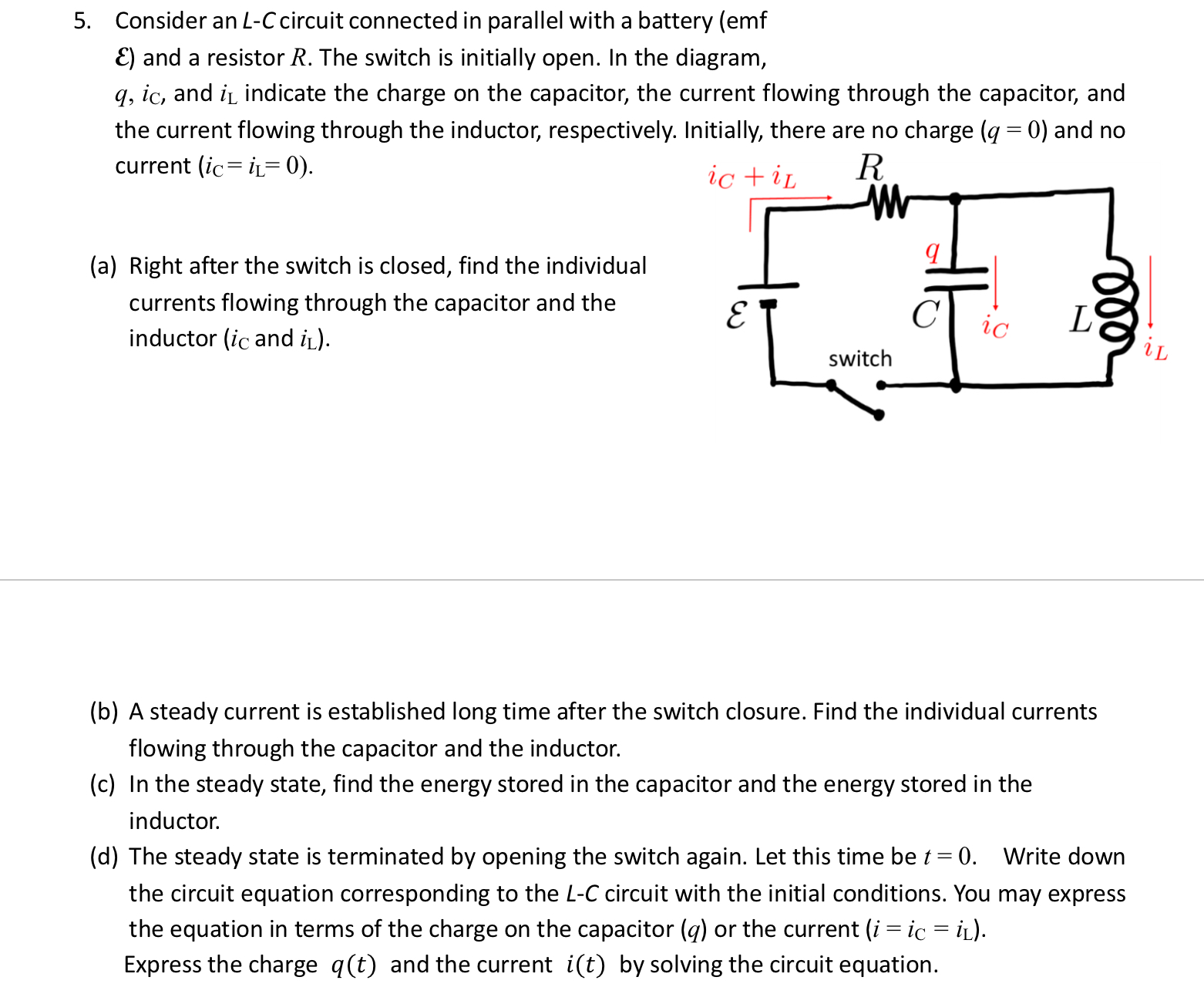
$5.$ Consider an L$-$C circuit connected in parallel with a battery $($emf

$\backslash (\backslash$mathcal$\{$E$\})\backslash )$ and a resistor $\backslash ($ R $\backslash ).$ The switch is initially open. In the diagram, $\backslash ($ q $\backslash ),\backslash ($ i$\_\{\backslash$mathrm$\{$C$\}\}\backslash ),$ and $\backslash ($ i$\_\{\backslash$mathrm$\{$L$\}\}\backslash )$ indicate the charge on the capacitor, the current flowing through the capacitor, and the current flowing through the inductor, respectively. Initially, there are no charge $\backslash (($q$=0)\backslash )$ and no current $(\backslash ($ i$\_\{\backslash$mathrm$\{$C$\}\}=$i$\_\{\backslash$mathrm$\{$L$\}\}=0\backslash )).$

$($a$)$ Right after the switch is closed, find the individual currents flowing through the capacitor and the inductor $(\backslash ($ i$\_\{\backslash$mathrm$\{$C$\}\}\backslash )$ and $\backslash ($ i$\_\{\backslash$mathrm$\{$L$\}\}\backslash )).$

$($b$)$ A steady current is established long time after the switch closure. Find the individual currents flowing through the capacitor and the inductor.

$($c$)$ In the steady state, find the energy stored in the capacitor and the energy stored in the inductor.

$($d$)$ The steady state is terminated by opening the switch again. Let this time be $\backslash ($ t$=0\backslash ).$ Write down the circuit equation corresponding to the L$-$C circuit with the initial conditions. You may express the equation in terms of the charge on the capacitor $\backslash (($q$)\backslash )$ or the current $\backslash (\backslash$left$($i$=$i$\_\{\backslash$mathrm$\{$C$\}\}=$i$\_\{\backslash$mathrm$\{$L$\}\}\backslash$right$)\backslash ).$ Express the charge $\backslash ($ q$($t$)\backslash )$ and the current $\backslash ($ i$($t$)\backslash )$ by solving the circuit equation.