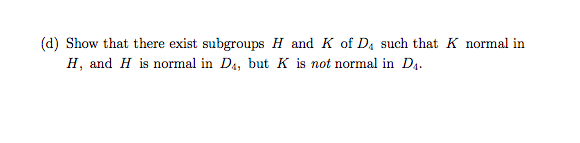
5. Consider the dihedral group DA = {(1), (1, 2, 3, 4), (1,3) (2, 4), (1, 4, 3, 2), (1, 2) (3, 4), (2, 4), (1, 4) (2,3), (1,3) } (a) List all subgroups of DA. How many nontrivial subgroups did you find? (Hint: You should find noncyclic subgroups.)(b) Find Z(D.). (You may list the elements without proof.) (c) Find all (nontrivial) normal subgroups of DA. (Hint: Problem 4 may be helpful. Also, you may use theorems proved in class.)(d) Show that there exist subgroups H and K of D, such that K normal in H, and H is normal in D., but K is not normal in DA