5 Elementary Calculus Questions

1.

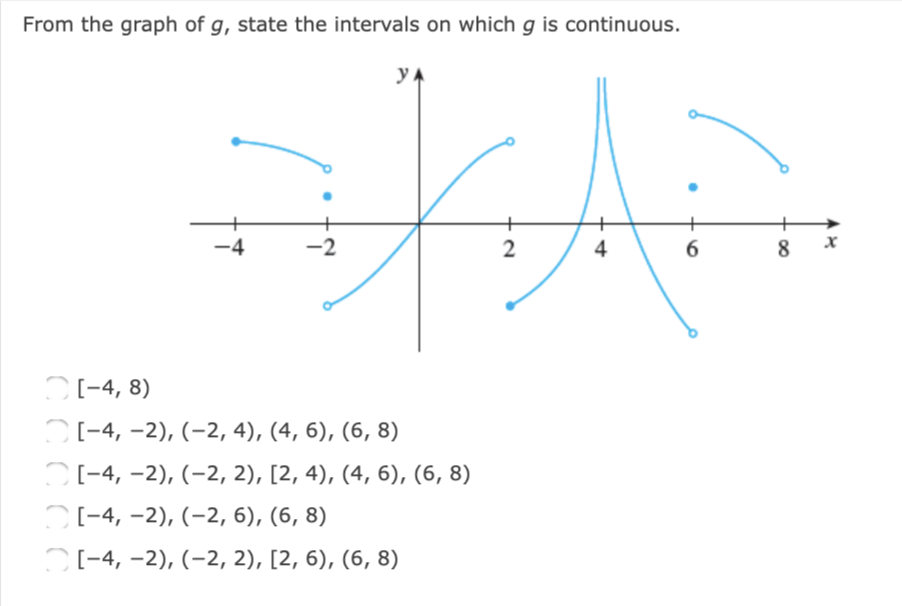
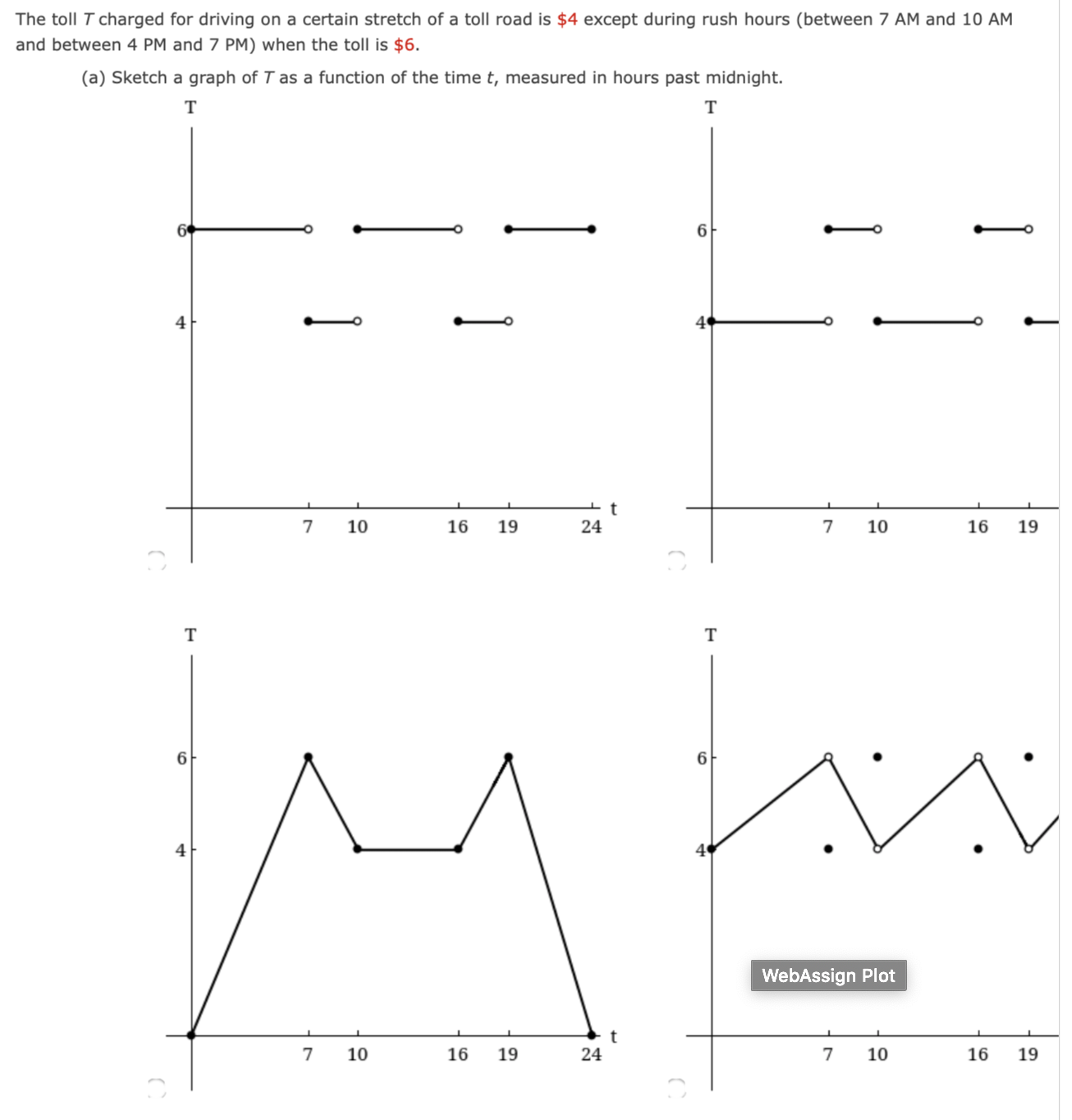
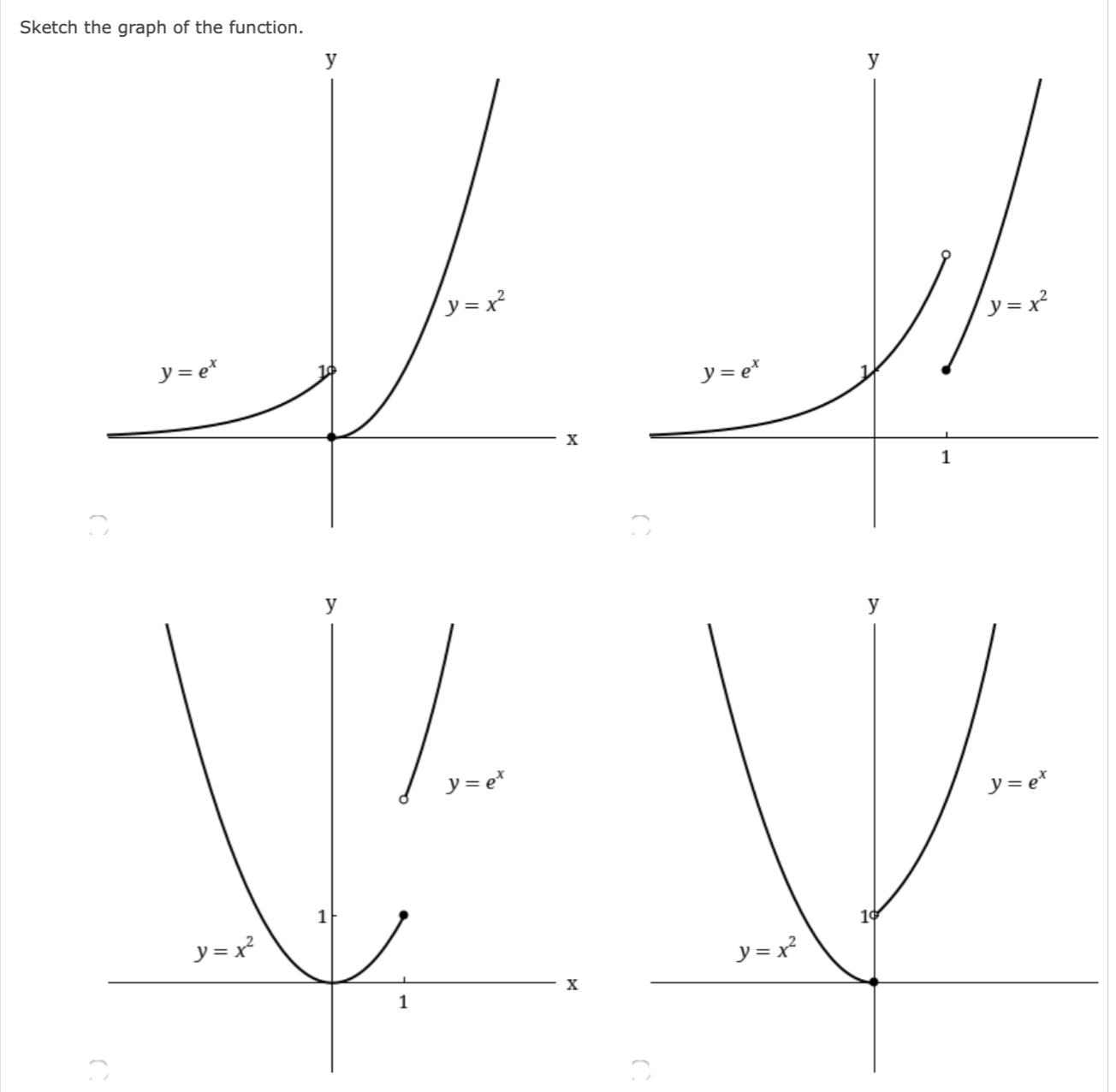
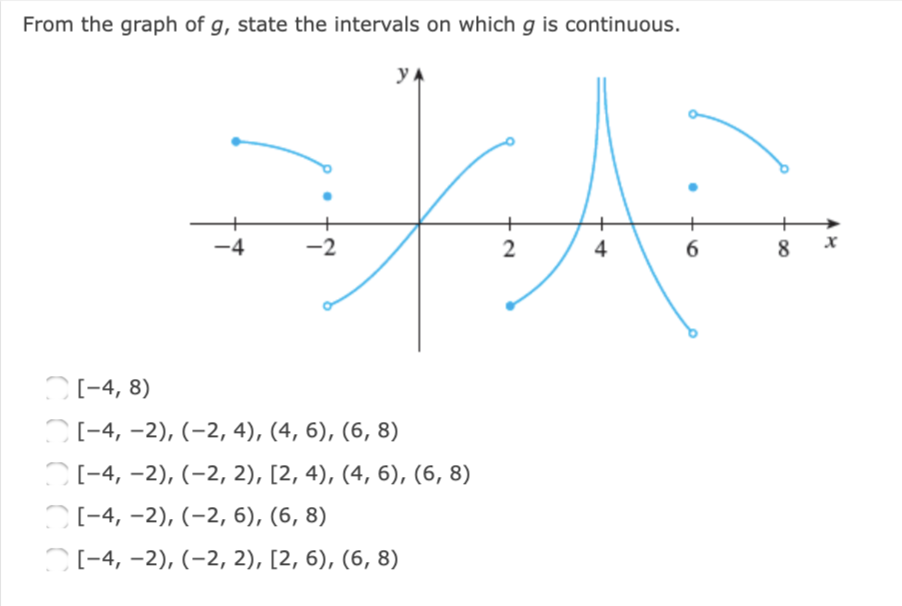
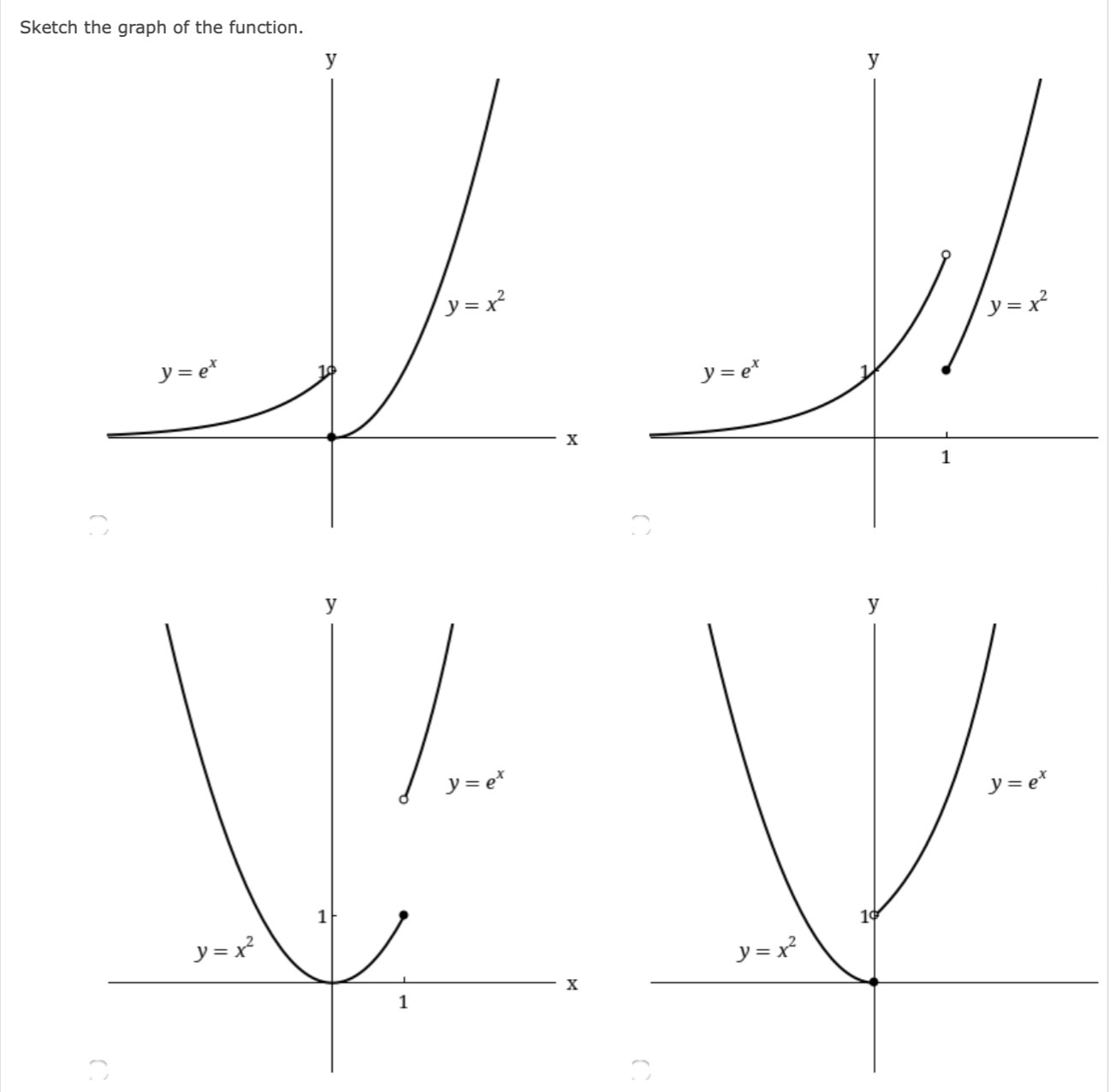
Given that x - 2 lim f(x) = 4 lim g(x) = -4 lim h(x) = 0, x - 2 find the limits, if they exist. (If an answer does not exist, enter DNE.) x - 2 (a) lim [f(x) + 3g(x)] (b) lim [g(x)13 x - 2 (C) lim vf(x) x - 2 (d) lim 5f(x ) x-2 g(x) (e) lim 9 ( x) x - 2 h(x) (f) lim g ( x)h(x) x - 2 f ( x )If fis continuous on (09, no), what can you say about its graph? (Select all that apply.) _ The graph of f has a hole. _ The graph of f has a jump. The graph of f has a vertical asymptote. none of these From the graph of g, state the intervals on which 9 is continuous. {-4: 3) I [4, 2), (2, 4), (4, 6), (6, 8) ' [4, 2), (2, 2), [2, 4), (4, 6), (6, 8) [4, 2), (2, 6), (6, 8) [4, 2), (2, 2), [2, 6), (6, 8) The toll Tcharged for driving on a certain stretch of a toll road is $4 except during rush hours (between 7 AM and 10 AM and between 4 PM and 7 PM) when the toll is $6. (a) Sketch a graph of T as a function of the time 1', measured in hours past midnight. 'I' 1' T T 6 6 o a 4 4 l o (b) Locate the discontinuities of T. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) t = Classify the discontinuities as removable, jump, or infinite. removable jump infinite none - T is continuous Discuss the significance of the discontinuities of 7 to someone who uses the road. Because of the sudden jumps in the toll, drivers may want to avoid the higher rates between t = 7 and t = 10 and between t = 16 and t = 19 if feasible. Because of the steady increases and decreases in the toll, drivers may want to avoid the highest rates at t = 7 and t = 24 if feasible. Because of the sudden jumps in the toll, drivers may want to avoid the higher rates between t = 0 and t = 7, between t = 10 and t = 16, and between t = 19 and t = 24 if feasible. The function is continuous, so there is no significance.Consider the following. f ( x ) = ex if x