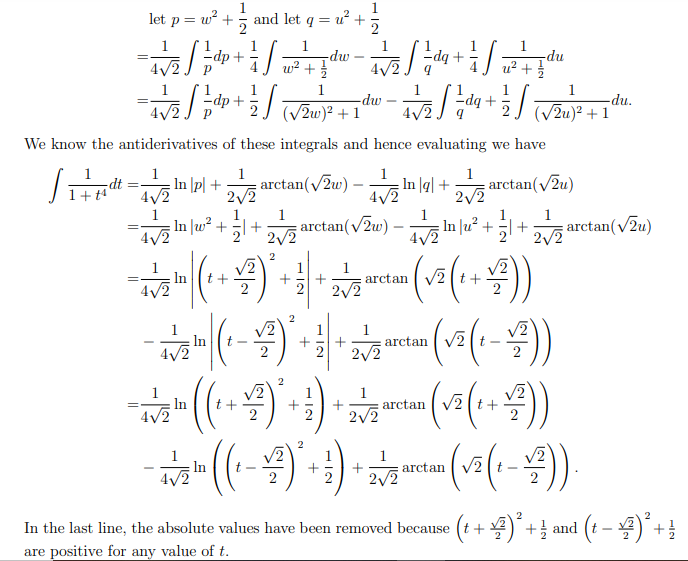
5. Find and explain the errors (if any) in the following solution. 1 We evaluate 1 + + adt by first factorizing the denominator as follows. Notice 1 + t' = (1 + (2)2 - 212 and factoring we have 1+t = (1+ +2)2 - 212 = (1+ +2 - V2t) (1 + +2 + V2t). Considering the concept of partial fractions we have 1 At + B Ct + D 12 + V2+ + 1 +2 - V2+ + 1 (which implies 1 = (At + B)(12 - v2+ + 1) + (Ct + D)(+ + v2t + 1)) where A, B, C and D are determined by solving the following system of equations 1 = B + D, 0 = A - V2B + C + V2D, 0 = -V2A + B+ V2C+D, 0 = A +C. The solution to this system of equations is A = -C= , B = D = :. We can now write 1 as1 t+ : 21/2 212 + 12 + 2t + 1 +2 - \\2t + 1 1 t+ v2 1 t - V2 2V2 (12 + V2t + 1) 2V/2 (t2 - V2t + 1) 1 t+ v2 1 t - V2 2V/2((t+ 43)2+ !) 2V/2 ((t - 42)2 + 4) pyright 2022 @ A. Chow and D. Yu where in the last line we completed the square. It follows that 1 1 + + v2 t - V2 -dt = -dt - 1 dt 2V/2 ((+ + V3)2+ }) 2V/2 ((t - 13)2+4) V2 let w =t+ and let u = t - 2 2 1/2 1 - 1/2 2 dw 2 du 2V/2 2V/2 191- 1 dw + dw du + du 2V2 W-+ 2 2V/2 u- + 2let p = w + and let q = u + P Ip + -dw - 4V/2 4V2 -dq + -du 12 + 1 dw (V2w)?+1 -dq + 2 du. AV (V2u)2+ 1 We know the antiderivatives of these integrals and hence evaluating we have 1 1 -dt In p + 4V/2 arctan(v2w) - 4V/2 In q + 2V/2 2V/2 arctan(v 2u) 1 arctan( v2w) 1 1 In w- + = + 412 2V/2 4V2 In lu- + 5+ 2V/2 arctan(v2u) 1 In t+ + + arctan 4V/2 21/2 (VZ (+ + 4 2 1 In V2 4V/2 2V/2 arctan v2 ( * - 2 2 1 1 In t . + 4V/2 2 2V/2 Arctan v2 ( 1+ 32) 2 + + 4v In 2V/2 arctan ( Vz (t - 2 2 ) In the last line, the absolute values have been removed because ( + 12 ) + 4 and + are positive for any value of t.