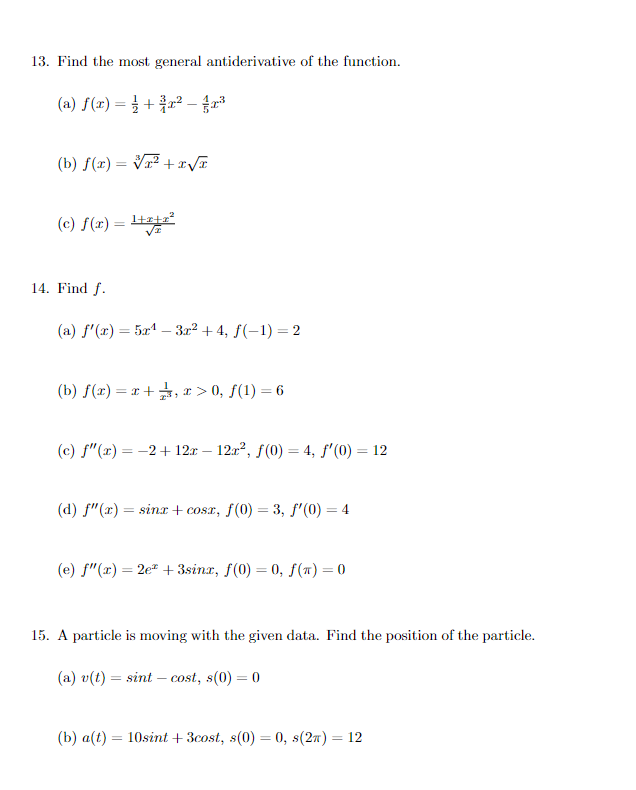
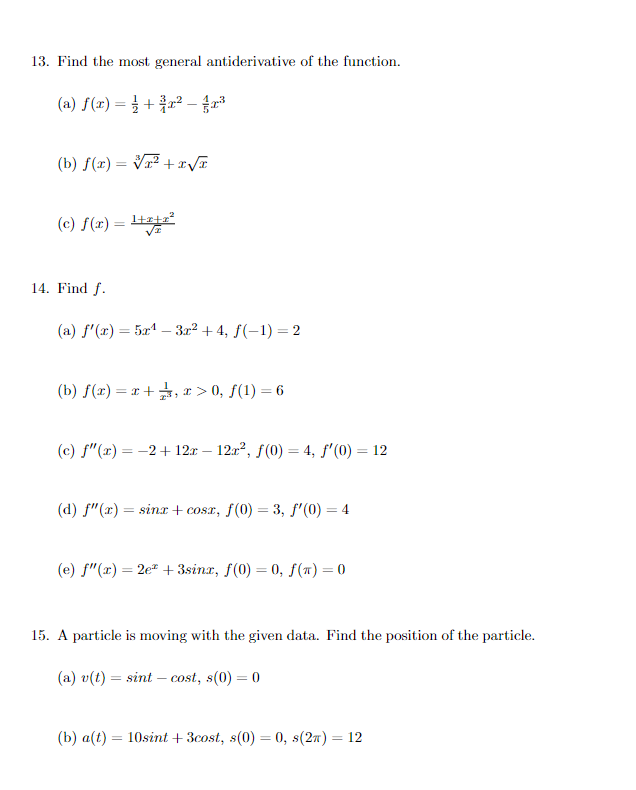
5. Find where the function is increasing or decreasing. Then find the local minimum and maximum values by using the First Derivative Test. (a) f(x) = 2x3 +3x2 - 12x (b) f(x) = (x -1)'(x+2) (c) f(x) = =+2 6. Find the local maximum and minimum values of f using both the First and Second Derivative Tests. (a) f(x) =x' +3x -8 (b) f(x) =12/3 -3 (c) f(x) = -2 - 12x2 -45x + 10 (d) f(x) = sin?(x) - cos(c); [", =]8. Find domain, intercepts, symmetry, asymptotes (if exists), intervals of increasing or decrease, local maximum and local minimum, concavity, in- flection points, and graph. (a) f(x) = 2cosr + cos x [0, 2x] (b) f(x) = 2 -3 I-2 (c) f(a) = - 12r+ 213. Find the most general antiderivative of the function. (a) f(x) = =+3x -4x (b) f(x) = Vrtax (c) f(x) = letz 14. Find f. (a) f'(x) = 5x1 - 3x2 + 4, f(-1) =2 (b) f(x) = x+ 4, x >0, f(1) =6 (c) f"(x) = -2+12x -12x2, f(0) = 4, f'(0) = 12 (d) f"(x) = sinx + cost, f(0) = 3, f'(0) =4 (e) f"(x) = 2et + 3sina, f(0) = 0, f(n) =0 15. A particle is moving with the given data. Find the position of the particle. (a) v(t) = sint - cost, s(0) = 0 (b) a(t) = 10sint + 3cost, s(0) = 0, s(2n) = 12