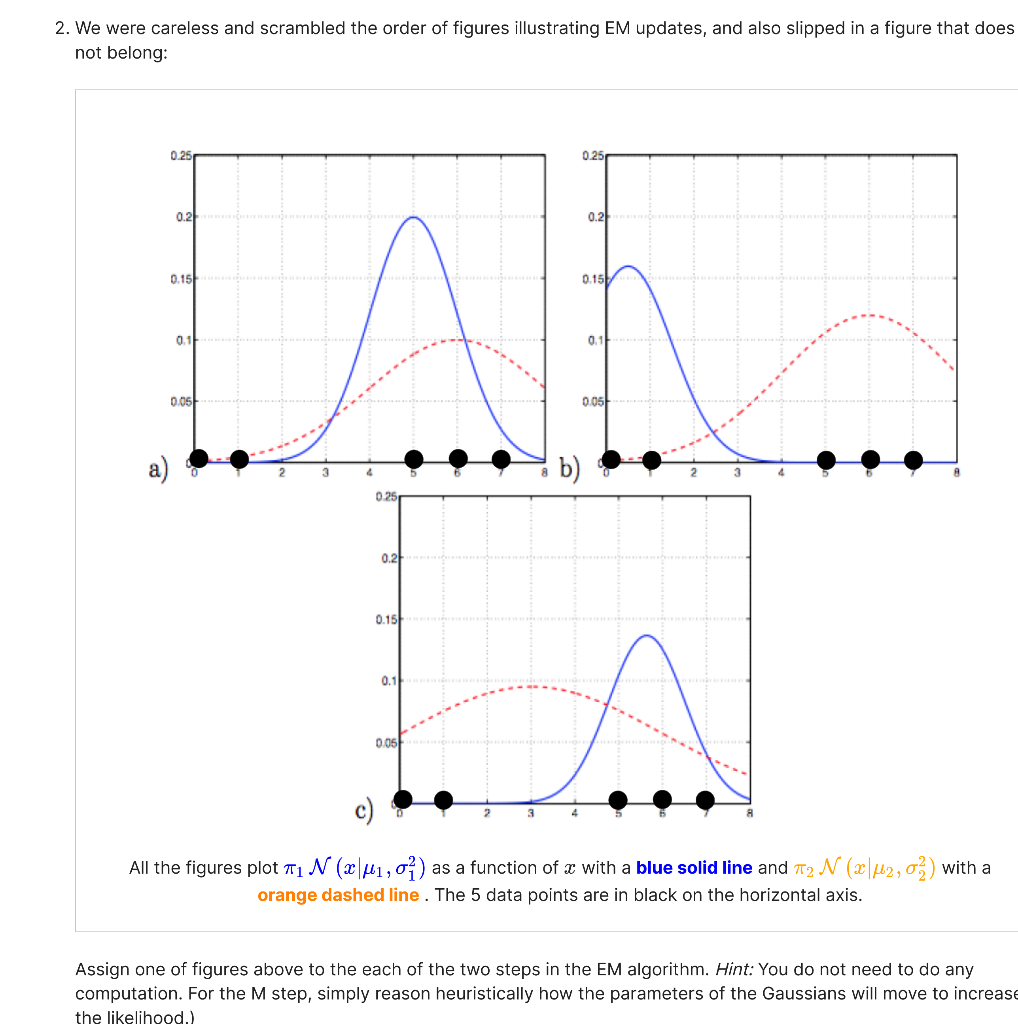
5. Gaussian Mixtures and EM algorithm Intuition D Bookmark this page Gaussian Mixtures and EM algorithm in 1D Suppose we are estimating a mixture of two Gaussians via the EM algorithm. The mixture distribution over x is given by P(x)=1N(x1,12)+2N(x2,22) 1. True or False: In the mixture model, we can identify the most likely posterior assignment, i.e., that a point x is more likely to belong to the first mixture or the second, by only comparing the values of 1N(x1,12) and 2N(x2,22). True False 2. We were careless and scrambled the order of figures illustrating EM updates, and also slipped in a figure that does not belong: 2. We were careless and scrambled the order of figures illustrating EM updates, and also slipped in a figure that does not belong: All the figures plot 1N(x1,12) as a function of x with a blue solid line and 2N(x2,22) with a orange dashed line. The 5 data points are in black on the horizontal axis. Assign one of figures above to the each of the two steps in the EM algorithm. Hint: You do not need to do any computation. For the M step, simply reason heuristically how the parameters of the Gaussians will move to increas the likelihood.) Step 0. Initial mixture distribution: figure a figure b figure C Step 1. After one EM-iteration: figure a figure b figure C