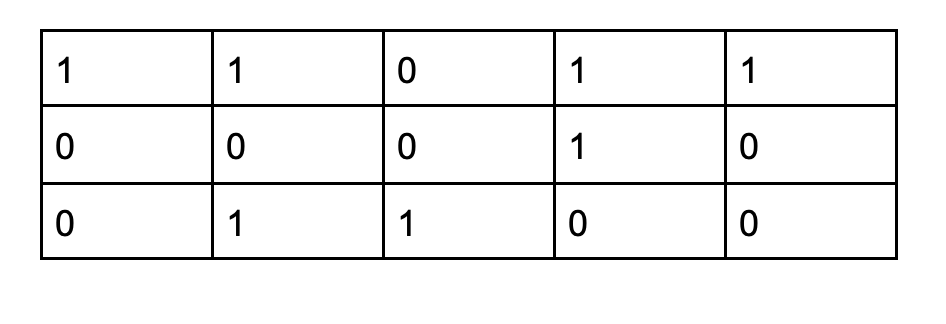
5. Given a m by n square grids. Suppose that each square is either land of water. An example is as follows, which shows a 4 by 5 grid with land squares filled with green and "water" squares filled with blue. Two "land" squares are considered in the same island if they are adjacent. In the above example, the grids has 3 different islands. Note that diagonal pairs of "lands are not considered adjacent. Describe an algorithm using pseudocode to output the number of "islands of a given m by n square grid. The running time of your algorithm should be O(mn). You may assume that the input is an m by n array. A[i,j] = 1 means that square [i,j] is land, and A[i,j] = 0 means that square [i,j] is water. Thus the above grid is given as: 1 1 0 1 1 0 0 0 1 0 O 1 1 0 0 0 0 1 0 0 Hint: Consider a graph with every land square as a vertex, and there is an edge connects every pair of adjacent lands. What are islands in this graph? You may modify the pseudocode for DFS/BFS in the slides, ALGORITHM DFS-WRAPPER(G) mark each vertex in V with O as a mark of being "unvisited count +O for each vertex v in v do if v is marked with O dfs(v) ALGORITHM dfs(v) count count + 1; mark v with count for each vertex w in V adjacent to v do if w is marked with O dfs(w) ALGORITHM BFS-Wrapper(G) mark each vertex in V with O as a mark of being unvisited count O for each vertex v in v do if v is marked with O bfs(v) bfs(v) count count + 1; mark v with count and initialize a queue with v while the queue is not empty do for each vertex w in V adjacent to the front vertex do if w is marked with O count count + 1; mark w with count add w to the queue remove the front vertex from the queue