Question: 5. Let f R2 R be a function defined by x+ y if y0; y f(x, y) = if y = 0. (a) Show

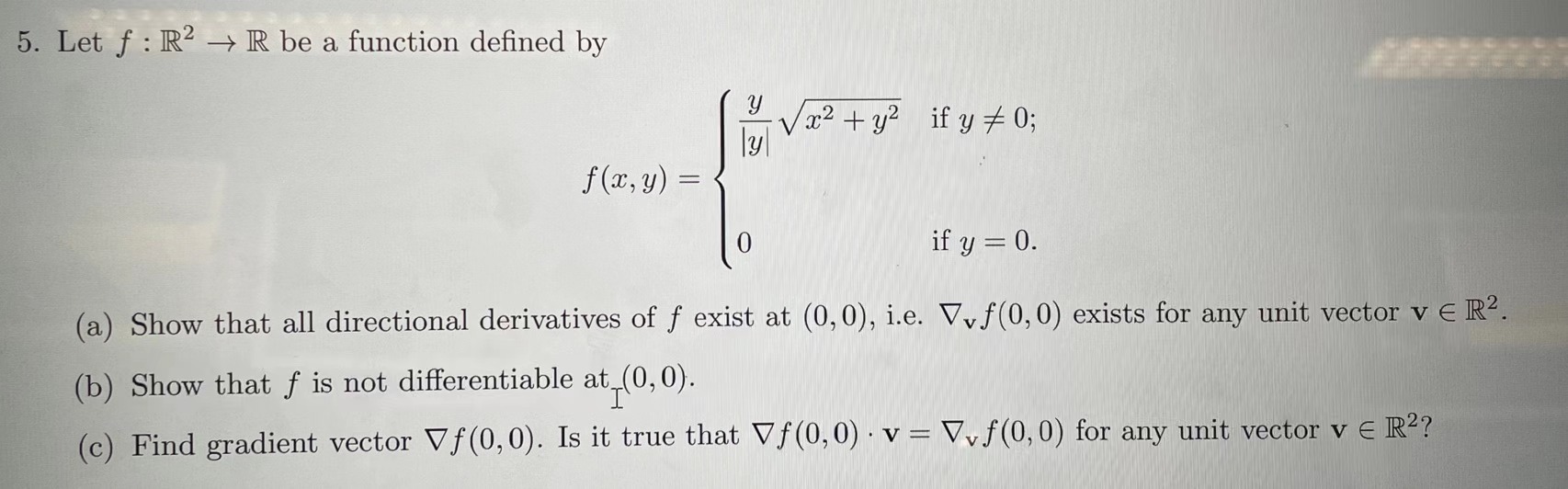
5. Let f R2 R be a function defined by x+ y if y0; y f(x, y) = if y = 0. (a) Show that all directional derivatives of f exist at (0,0), i.e. Vvf(0,0) exists for any unit vector v R. (b) Show that f is not differentiable at (0,0). (c) Find gradient vector Vf (0, 0). Is it true that Vf(0,0) v=Vvf(0,0) for any unit vector v R?

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

For May 2021 Husky Baking budgeted to produce 500 wedding cakes and budgeted the following: Employee Class Hours Cost per Hour Total Cost Baker 450 $ 20 $ 9,000 Baker Assistant 600 $ 16 $ 9,600 In...

Question: Check you are in charge of the design of both hardware and software for a new (but fairly conventional) workstation which will have its peripherals (for example a disc drive and a printer)...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

A machine fills containers with a particular product. The standard deviation of filling weights computed from past data is 0.6 ounces. If only 2% of the containers hold less than 18 ounces, what is...

Andy Frain is an audit senior of a large public accounting firm who has just been assigned to the Usher Corporations annual audit engagement. Usher is a public company and has been a client of Frains...

Show a snippet of PHP code for creating a RecordSet. Explain the meaning of the code.

What are the null and alternative hypotheses tested by the ????-ratio in the ANOV table?

Hotel XYZ is an independent city centre hotel property with 200 rooms. In general its Average Daily rate is approximately 100 throughout the year, and its runs at an average of 65% occupancy. Its...

a) The following financial information regarding Wick Industries is available. Total liabilities $150 000 Total equity 400 000 Total assets 550 000 Income tax expense 20 000 Net income 35 000...

In Problem 18, suppose Belyk Paving Co. paid out $370,000 in cash dividends. Is this possible? If net capital spending was zero, no new investments were made in net working capital, and no new stock...

Barberry, Inc., manufactures a product called Fruta. The company uses a standard cost system and has established the following standards for one unit of Fruta: During June, the company recorded this...

Question 4. Fashion Extended bought some inventory from Calvin Klein in 2020 for $540,000 on credit terms and paid for the inventory in 2021. In 2021 Fashion Extended sold $315,200 of the inventory...

.80 80 Create the part shown in the orthographic multi-view drawing. Verify that you have the mass correct, then input the SURFACE AREA below. Units: IPS Part Origin: Arbitrary Material: ABS Mass:...

Keiras Kar Company purchases a Machine and incurs the following costs: Purchase Price $250,000 Sales Tax $5,000 Installation Cost $1,500 Electricity Costs for the Year $2,000 Deliver Costs $500...

Tommy Lee is recovering from a drug addiction problem. His employer has offered him services to help him with the recovery process. What is this service an example of ? a . an outplacement service b...

Absorption vs. variable costing Reese's Tot Toy Boxes uses variable costing to manage its internal operations. The following data relate to the company's first year of operation, when 30,000 units...

Primare Corporation has provided the following data concerning last month's manufacturing operations. Purchases of raw materials Indirect materials included in manufacturing overhead $ 4,590 Direct...

The words without recourse on an indorsement means the indorser is: a. not liable for any problems associated with the instrument. b. not liable if the instrument is dishonored. c. liable personally...

Problem 2.19. A material is found to have a thermal expansivity ap = (R/Pv)+ (a/RT2v) and an isothermal compressibility T = (1/v)(Tf(P)+(b/P)), where v (V/n) is the molar volume. (a) Find f(P). (b)...

Problem 2.21. It is found for a gas that T = Tvf (P) and ap = (Rv/P) + (Av/T), where T'is the temperature, v is the molar volume, P is the pressure, A is a constant, and f(P) is an unknown function...

Problem S2.8. Consider the reaction 2NH3 = N2 + 3H2, which occurs in the gas phase. Start initially with 2 mol of NH3 and 0 mol each of H and N2. Assume that the reaction occurs at temperature 7 and...