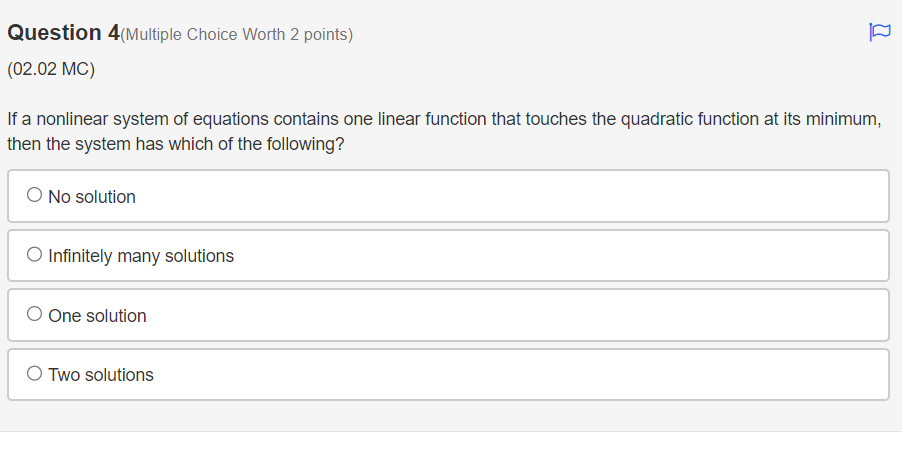
Question: 5- Question 4(Multiple Choice Worth 2 points) F3 (02.02 MC) If a nonlinear system of equations contains one linear function that touches the quadratic function
5-
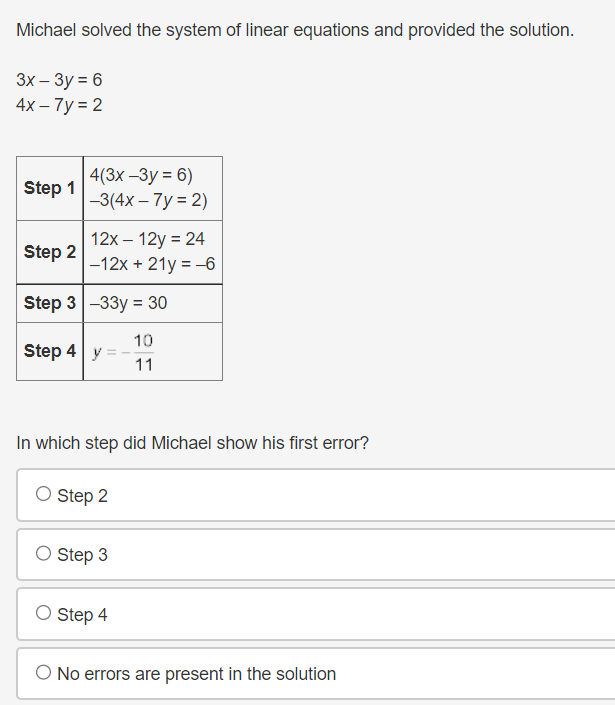
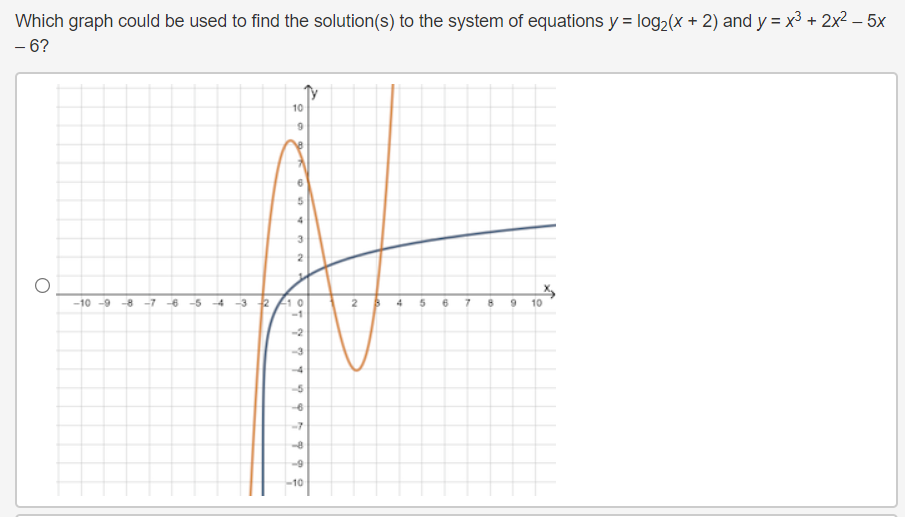
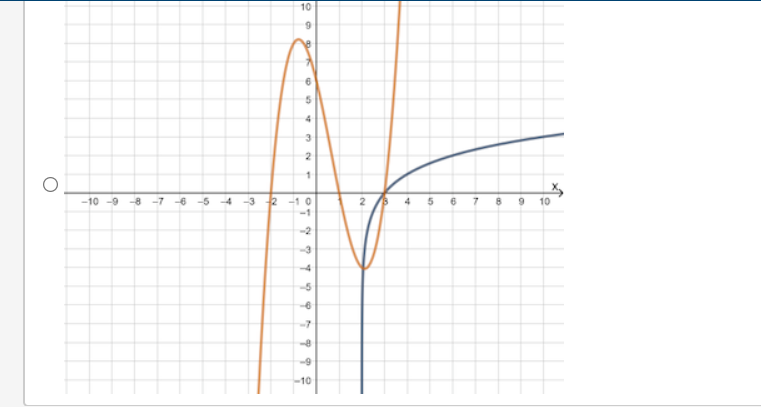
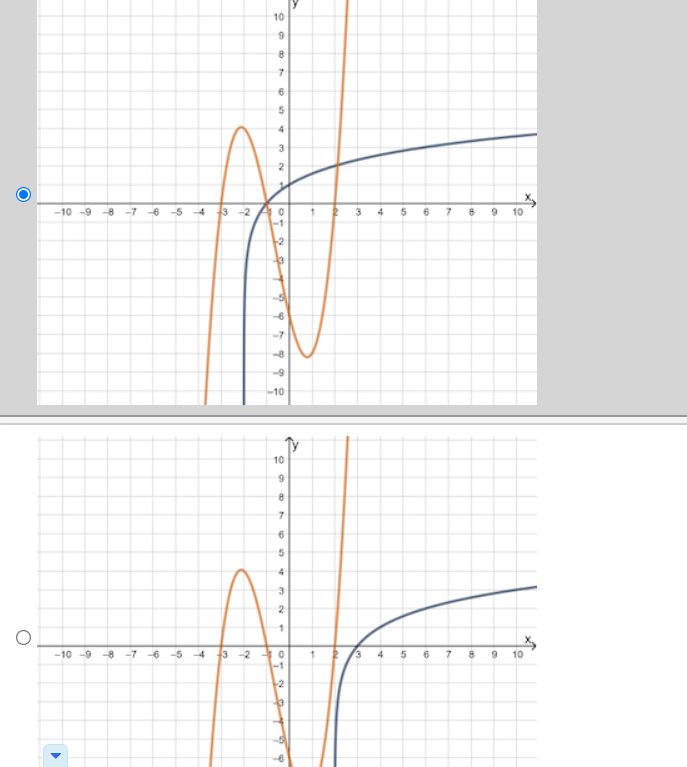
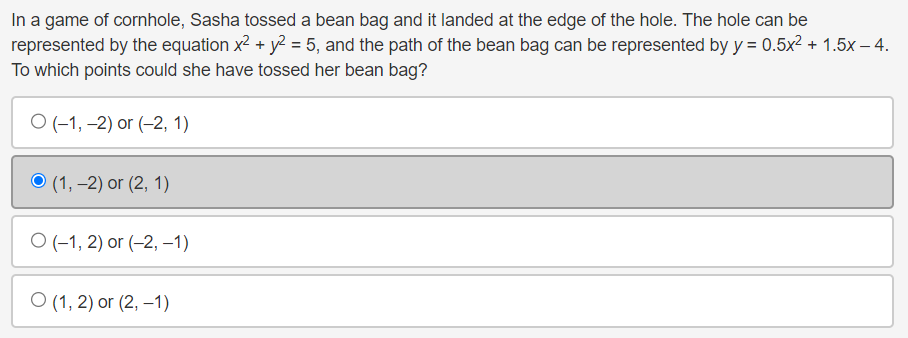
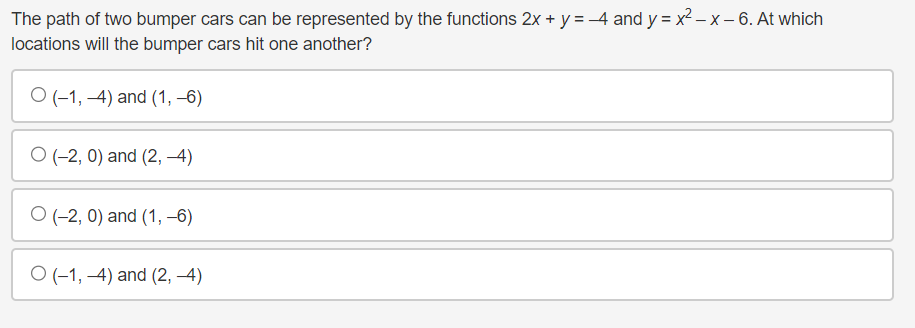
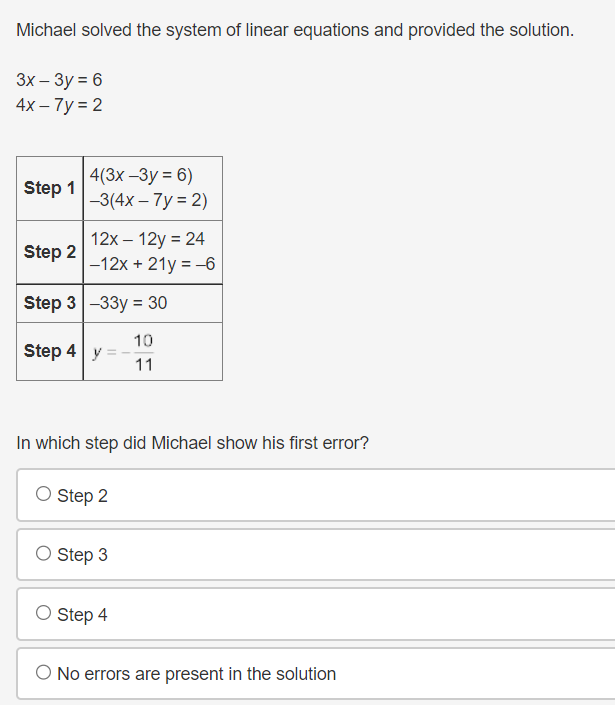
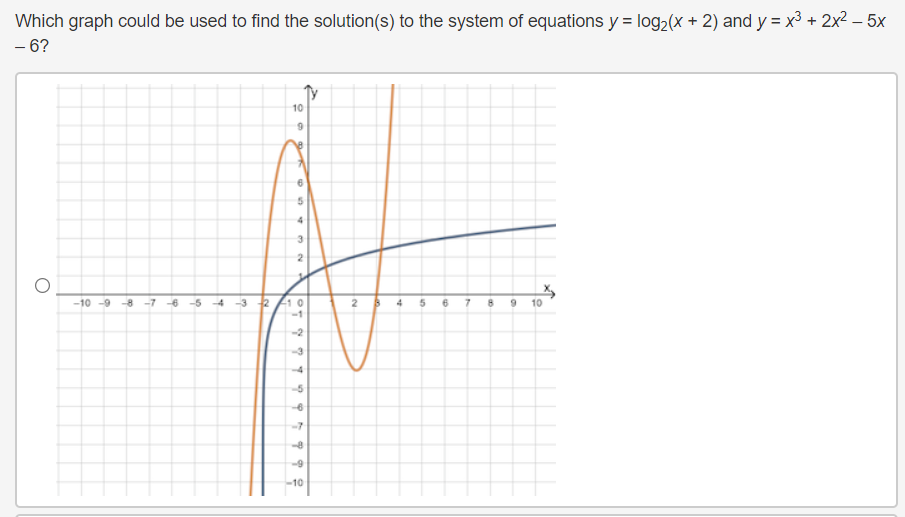
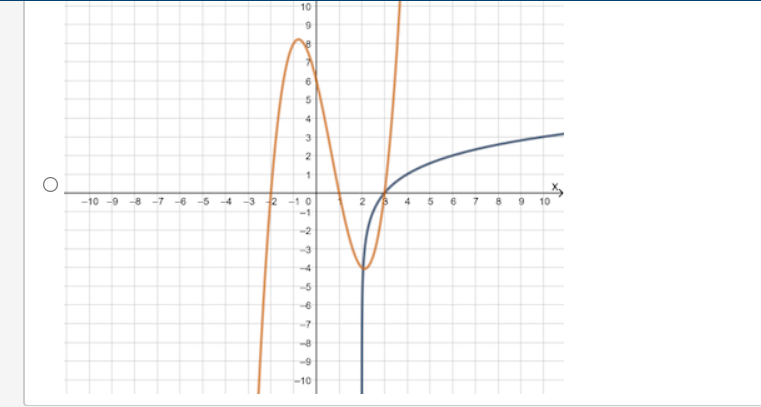
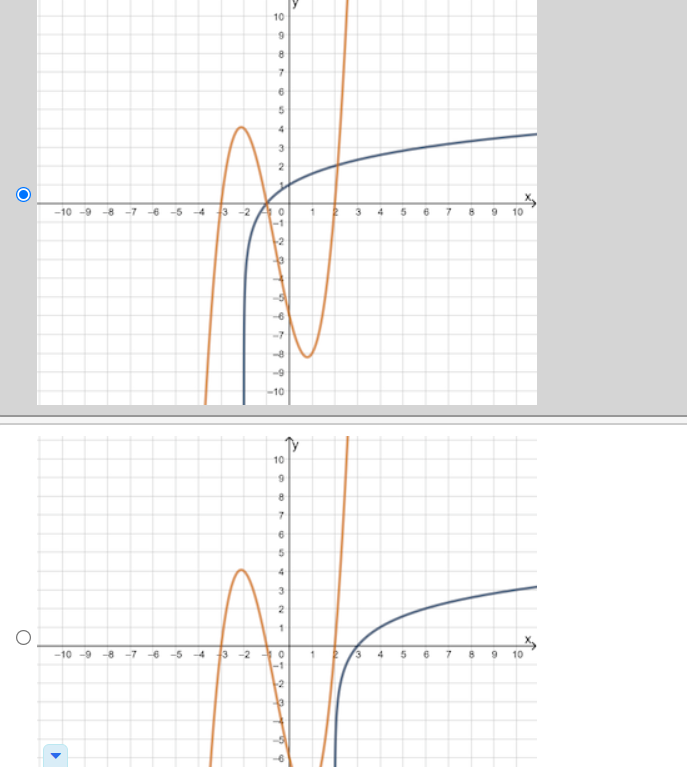
Question 4(Multiple Choice Worth 2 points) F3 (02.02 MC) If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has which of the following? 0 No solution 0 Innitely:r many solutions O One solution 0 Two solutions Michael solved the system of linear equations and provided the solution. 3x - 3y = 6 4x - 7y = 2 4(3x -3y = 6) Step 1 -3(4x - 7y = 2) 12x - 12y = 24 Step 2 -12x + 21y = -6 Step 3 -33y = 30 10 Step 4 V= 11 In which step did Michael show his first error? O Step 2 O Step 3 O Step 4 O No errors are present in the solutionWhich graph could be used to find the solution(s) to the system of equations y = log2(x + 2) and y = x3 + 2x2 - 5x - 6? 10 O -10 -9 8 -7 6 5 4 3 2 N 4 5 6 7 8 9 10In a game of oornhole, Sasha tossed a bean bag and it landed at the edge of the hole. The hole can be represented by the equation x2 + y2 = 5, and the path of the bean bag can be represented by y: 0.5-):2 + 1.5x 4. To which points could she have tossed her bean bag? 0 (1, 2) or (2. 1) (1,2)or(2,1} O (1, 2} or (2, 1) O (1, 2) or (2, '1) The path of Mo bumper cars can be represented by the functions 2X + y = 4 and y = x2 X 6. At which locations will the bumper cars hit one another? 0 (1, 4) and n: 45) O (2, o) and (2, 4) O (2, o) and (1, 4)) O (1, 4) and (2: 4)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


