Question: Suppose the sequence {an}1 converges to L and that the set {an |n e N} has infinitely many values. Prove that L is the

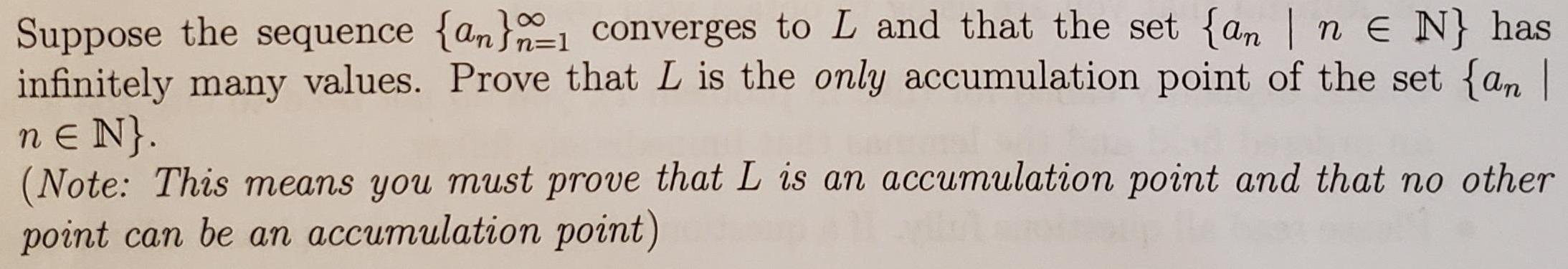
Suppose the sequence {an}1 converges to L and that the set {an

Suppose the sequence {an}1 converges to L and that the set {an |n e N} has infinitely many values. Prove that L is the only accumulation point of the set {an | ne N}. (Note: This means you must prove that L is an accumulation point and that no other point can be an accumulation point)

Step by Step Solution

★★★★★

3.54 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The sequence an L Convenges to L If possiblelet LfL be two Qccu mu la... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Prove that if a sequence converges in distribution to a constant value, then it also converges in probability. This one together constitute an alternative proof to the weak law of large numbers.

Suppose that ak 0. Prove that k=1 ak converges if and only if the series k=1 (a2k + a2k+1) converges.

Suppose that you can lift no more than 650 N (around 150lb) unaided. (a) How much can you lift using a 1.4-m-long wheelbarrow that weighs 80.0 N and whose center of gravity is 0.50 m from the center...

Prove that protocol OddEven-MergeSort is a sequence of 1 + log n iterations and that in each iteration (except the last) every data item is sent once or twice to another entity.

An AR(3) process {x(n)} is characterized by the autocorrelation sequence xx(0) = 1, xx(1) = , xx(2) = 1/8, and xx(3) = 1/64. (a) Use the Schur algorithm to determine the three reflection coefficients...

CVP analysis, shoe stores refer to requirement 3 of Problem 3-38. In this problem, assume the role of the owner of Walk Rite. If you want to use Excel to solve this problem, go to the Excel Lab at...

CVP analysis, shoe stores (continuation of 3-38). Refer to requirement 3 of Problem 3-38. In this problem, assume the role of the owner of WalkRite. 1. Calculate the number of units sold at which the...

1. Which of the following are not included in GDP? a. Leisure time b. Sales of new cars c. Strawberries sold in a grocery store d. Economics textbooks sold in the bookstore 2. Men s reported...

Use the following normal- form game to answer the questions below. a. Identify the one- shot Nash equilibrium. b. Suppose the players know this game will be repeated exactly three times. Can they...

Refer to requirement 3 of Problem 3- 28. In this problem, assume the role of the owner of Dress4Less. Required 1. Calculate the number of units sold at which the owner of Dress4Less would be...

A company produces a product that requires 2.5 standard pounds per unit. The standard price id $3.75 per pound. If 5,000 units require 36,000 pounds, which were purchased at $4.00 per pound, what is...

A manufacturing company has recently outsourced its entire operations processes. Moreover, the CEO has decided to start an e-commerce business model to find a new market to target consumers with...

Primary source analysis. There are three newspaper excerpts included in the Election of 1800 section of the lesson. For each source, identify if it was a Republican newspaper (in favor of the...

Discuss the ECCO Case. In your discussion, please make sure to address the following questions: What sets ECCO's supply chain apart from their competitors? How do you think that they can improve it...

Best Vision is revamping its assembly lines to improve efficiency. As shown below, there are 10 steps to assembling a television set. Best Vision needs to produce 125 televisions in a 40-hour work...

Colby Company reports net income of $50,000. For the year, depreciation expense is $15,000 and the company reports a gain of $5,000 from sale of machinery. It also had a $3,000 loss from retirement...

Question on Call spreads and digital options: [Source: Intro to Quantitative Finance by Stephen Blyth, Chapter 7 Exercise 4] (a) Draw the payout profile for the following two call spread portfolios....

According to a New York Times columnist, The estate tax affects a surprisingly small number of people. In 2003, . . . just 1.25 percent of all deaths resulted in taxable estates, with most of them...

An at-the money call written on a stock with current price St = 100 trades at 3. The corresponding at-the money put trades at 3.5. There are no transaction costs and the stock does nor pay any...

Plot the payoff diagrams fur the following instruments: (a) A caplet with cap rate Rcap = 6.75% written on 3-wonth Libor Lt, that is about to expire. (b) A forward contract written on a default-free...

Using the data in the previous question, you are now asked to approximate the current value of a European call option on the stock St. the option has a strike price of 100, and a maturity of 100 days...

Take a sheet of paper and make six columns on it. Label the columns mere disagreements, overblown conflicts, competition, verbally abusive conflicts, and physically abusive conflicts. In each column,...

Can you think of examples where people either focused on the other person or tried to deal with the problem or issue instead? Discuss the outcomes.

For the above case, write out at least four statements that demonstrate fractionation, framing, reframing, and common ground.