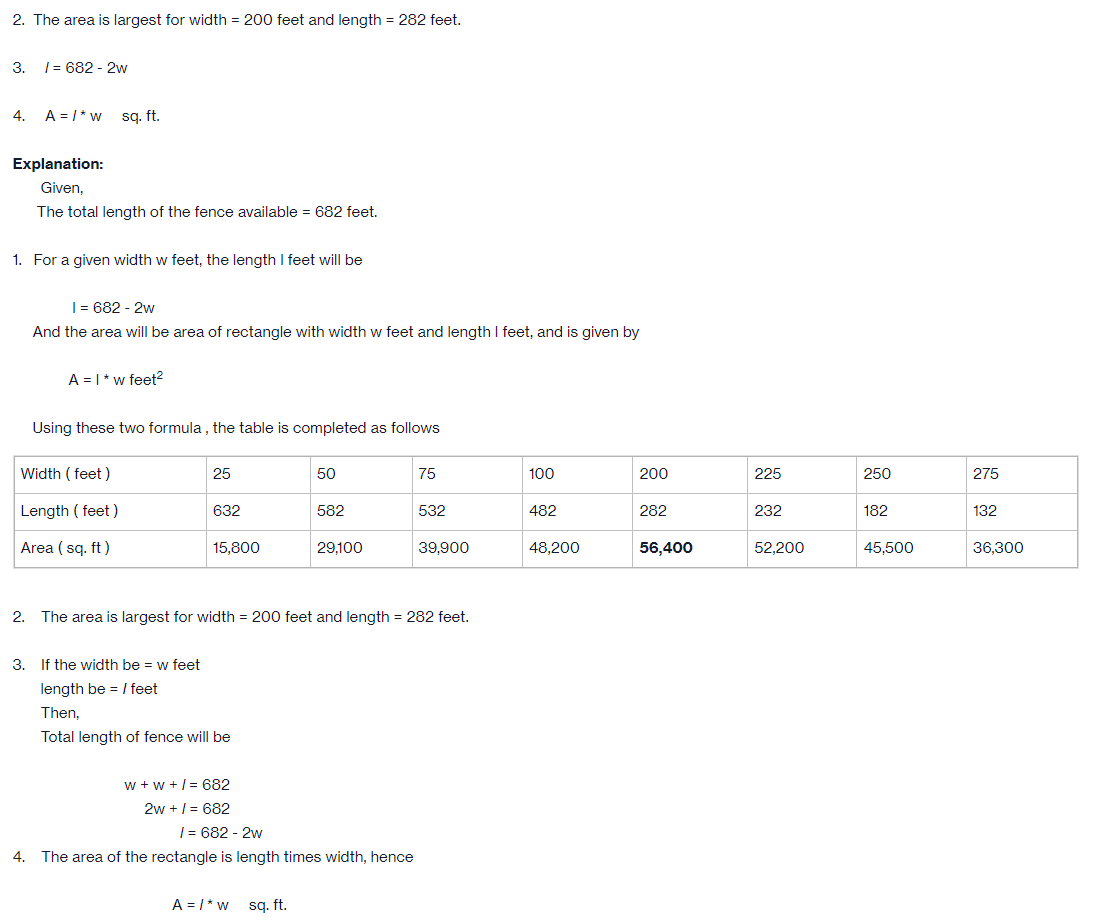
5. Use the general formula to write the area A of the enclosure as a function of w (that is, only the variable w should appear in the function). Write the function in simplest form. What type of function is this? 6. Use your calculator to obtain a graph of the area function. Choose a window that shows both horizontal intercepts and the vertex. Locate the point on your graph that represents your answer to Question 2 by letting Y, = the corresponding area, then finding the intersection. (Note there will be two intersections, you must choose the correct one). Draw an arrow pointing to the point that represents your answer to Question 2, and write the coordinates as an ordered pair. Go to the Math Lab or library and either obtain a printout of the screen or copy it to the clipboard and paste it into your WORD document. In either case, label the axes with variable and word labels, and label the tic marks on each axis. Look at the window on your graphing calculator to help with this. Label the graph with its function. Give your graph a title. Write the window settings you used: Xmin, Xmax, Xsel, Ymin, Ymax, Ysel. 7. What do we call the graph of this area function? 8. What is the name of the point that represents the maximum area? 9. Find the width needed to give the maximum area algebraically. Show the formula you used and the steps to the solution. Express your answer with appropriate unit. 10. Now that you know the width needed to find the maximum area, find the corresponding length of the enclosure of maximum area using the formula from question 3. Show the steps to your solution. Express your answer with appropriate unit. 11. Now find the maximum area algebraically using the function A(w) . Express your answer with appropriate unit.2. The area is largest for width = 200 feet and length = 282 feet. 3. i: 882 - 2w 4. A=i*w sq.ft. Explanation: Given. The total length of the fence available = 682 feet. 1. For a given width w feet. the length I feet will be |=6822w And the area will be area of rectangle with width w feet and length l feet, and is given by A=|*wfeet2 Using these two formula, the table is completed as follows Width ( feet } 25 50 7'5 100 200 225 250 275 Length ( feet } 632 582 532 482 282 232 182 132 Area [ sq. ft) 15,800 29,100 39,900 48,200 56,400 52,200 45,500 36,300 2. The area is largest for width = 200 feet and length = 282 feet. 3. If the width be = w feet length be = i feet "hen. "otal length of fence will be w + w + i = 682 2w + i = 882 i: 682 2w 4. The area of the rectangle is length times width, hence A=i*w sq.ft