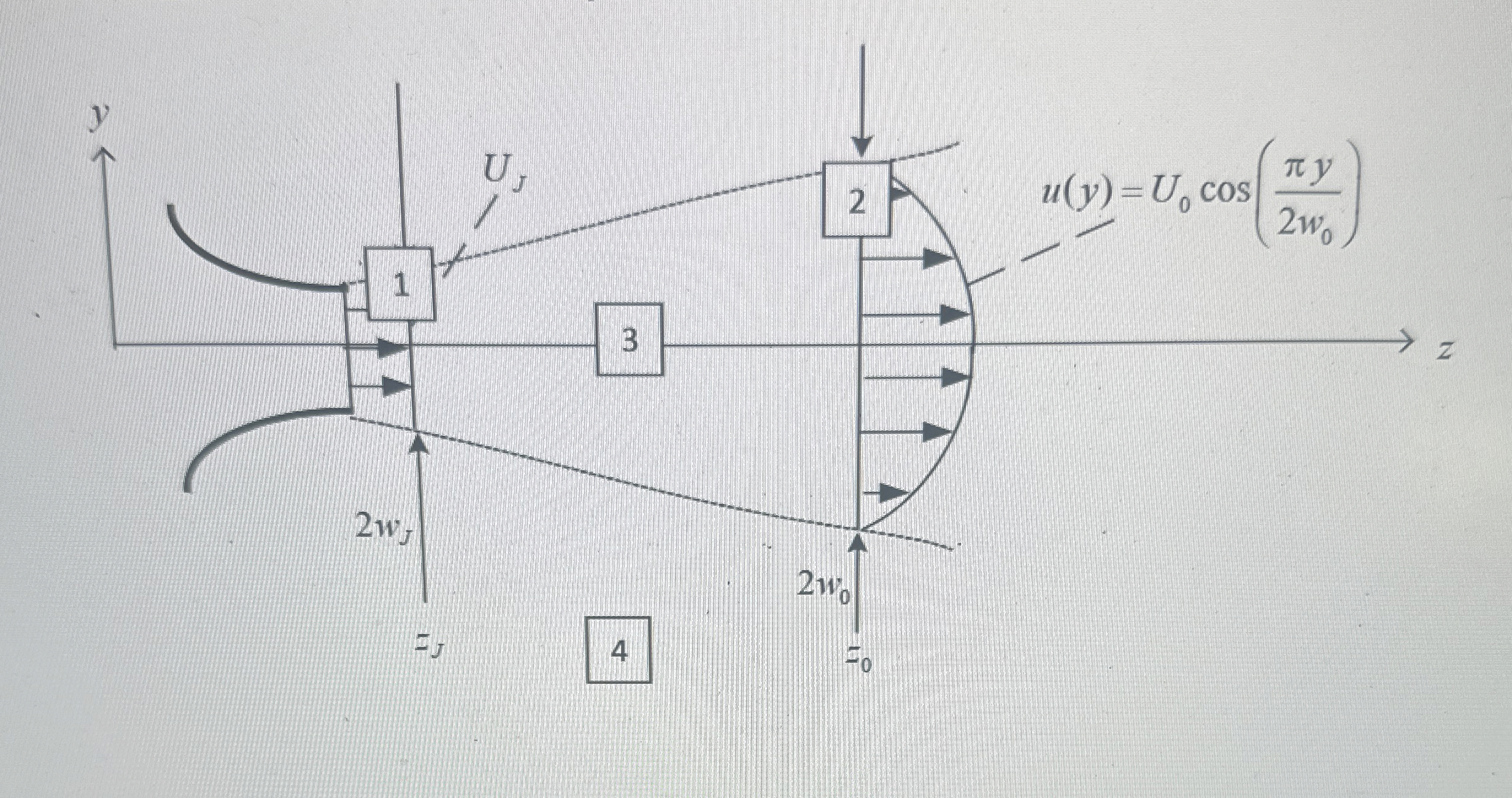
$6\mathrm{.}4$ A two$-$dimensional, inviscid jet ejects from a nozzle into a quiescent ambient as shown below. z is the axial direction and $y$ is the transverse direction with the jet centerline being $y=0.$ Consider the depth of the jet into the page to be equal to $b.$ The flow and ambient fluid have the same density $.$ Immediate downstream from the jet exit $z_J,$ the jet assumes a uniform axial velocity $U_J$ and a half$-$width $w_J($both given$).$ Some distance $z_0$ downstream from the jet exit, the jet has expanded to a half width $w_0($given$)$ and has an axial velocity profile: $u(y)=U_{0}cos(\frac{y}{2w_0}),$ where $U_0$ is unknown. Assume a constant ambient pressure everywhere outside of the nozzle exit.

There are two well$-$known characteristics of inviscid jet flows. First, they have a constant momentum flux $($explain why$).$ Second, they entrain a large amount of ambient fluid as they spread.

These trigonometric integration relations might be useful: ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}si{n}^2(ax)dx=\frac{x}{2}-\frac{sin(2ax)}{4a}{\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}co{s}^2(ax)dx=\frac{x}{2}+\frac{sin(2ax)}{4a}$

Use the control volume enclosed by four control surfaces II to $4$ as shown below, identify all forces as well mass flux acting on these surfaces.

Determine the centerline velocity $U_0$ but not using the mass conservation here. Explain why we cannot use the mass conservation.

Determine the mass flux of ambient fluid being entrained into the jet $m_3^{}+m_4^{}.$

What do the centerline velocity will behave downstream if $w_0{z}^{\frac{2}{3}}.$Use the control volume enclosed by four control surfaces $1$ to $4$ as shown below, identify all forces as well mass flux acting on these surfaces.

Determine the centerline velocity $U_0$ but not using the mass conservation here. Explain why we cannot use the mass conservation.

Determine the mass flux of ambient fluid being entrained into the jet $m_3^{}+m_4^{}.$

What do the centerline velocity will behave downstream if $w_0{z}^{\frac{2}{3}}.$