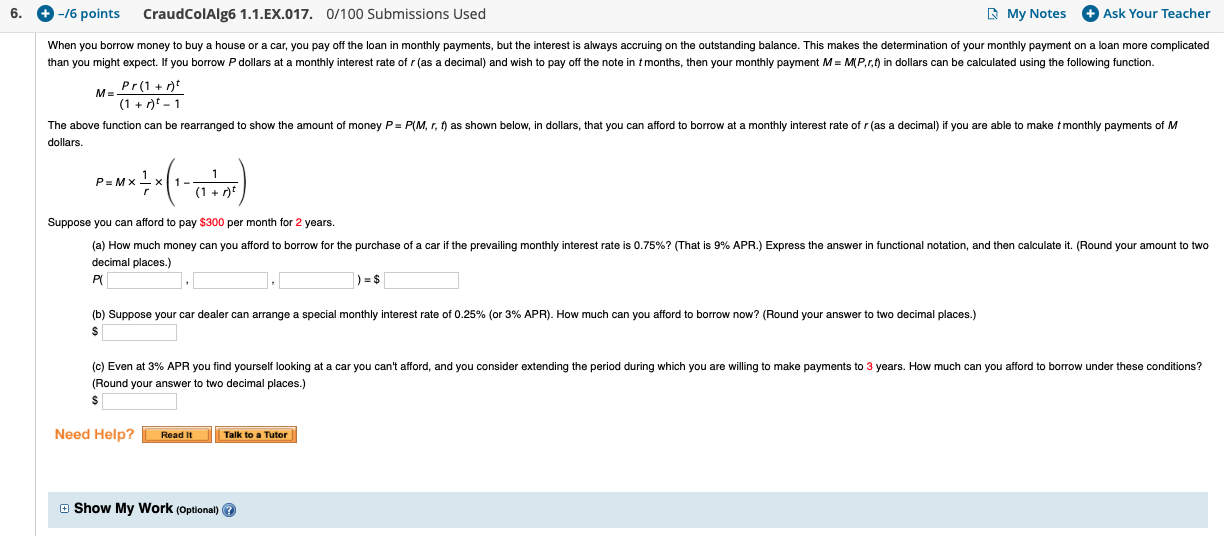
6. -/6 points CraudColAlg6 1.1.EX.017. 0/100 Submissions Used My Notes + Ask Your Teacher When you borrow money to buy a house or a car, you pay off the loan in monthly payments, but the interest is always accruing on the outstanding balance. This makes the determination of your monthly payment on a loan more complicated than you might expect. If you borrow P dollars at a monthly interest rate of r(as a decimal) and wish to pay off the note in t months, then your monthly payment M = MP,r,t) in dollars can be calculated using the following function. M-Pr(1 + r) (1 + n)-1 The above function can be rearranged to show the amount of money P= P(M,r, t) as shown below, in dollars, that you can afford to borrow at a monthly interest rate of r(as a decimal) if you are able to make t monthly payments of M dollars. Suppose you can afford to pay $300 per month for 2 years. (a) How much money can you afford to borrow for the purchase of a car if the prevailing monthly interest rate is 0.75%? (That is 9% APR.) Express the answer in functional notation, and then calculate it. (Round your amount to two decimal places.) ) = $ (b) Suppose your car dealer can arrange a special monthly interest rate of 0.25% (or 3% APR). How much can you afford to borrow now? (Round your answer to two decimal places.) (c) Even at 3% APR you find yourself looking at a car you can't afford, and you consider extending the period during which you are willing to make payments to 3 years. How much can you afford to borrow under these conditions? (Round your answer to two decimal places.) Need Help? Read It Talk to a Tutor Show My Work (Optional)