Question: (6) Let TE C(P(R) ) be defined by T(p(x)) = 3p(x) - up'(x). Let U be the 7-cyclic subspace of P(R) generated by q(x) =

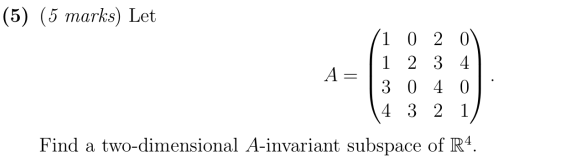
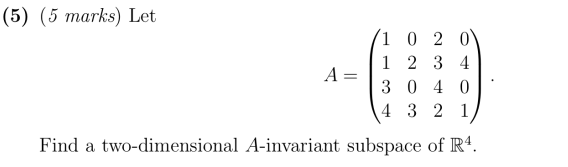
(6) Let TE C(P(R) ) be defined by T(p(x)) = 3p(x) - up'(x). Let U be the 7-cyclic subspace of P(R) generated by

such that 8 = {q, T(q), . ... T"-'(q)} is a basis

(6) Let TE C(P(R) ) be defined by T(p(x)) = 3p(x) - up'(x). Let U be the 7-cyclic subspace of P(R) generated by q(x) = r* + 2r. (i) (4 marks) Determine the integer n such that 8 = {q, T(q), . ... T"-'(q)} is a basis for U. (ii) (4 marks) Find the matrix representation [7], where 8 is the ordered basis in (i).

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

HELP! HI, I am supposed to create a 2d array with the alphabet shown below, I was able to get the table exactly but I am not using the methods as I am supposed to... here ir what I have so far please...

AutoSave OFF AESU Investment quiz.2020-4.xls - Compatibility Mode Q- poi Home Insert Draw Page Layout Formulas Data Review View Tell me Share Comments X Arial v A v 10 Insert v ab Wrap Text Ceneral...

Encryption and Decryption Using the Vigenere Cipher The Vigenere Table has been entered in cells A2 thru Z27 of the Lab3 spreadsheet. Encryption 1. Enter the encryption/decryption key (up to 7...

The research firm LL Research collected data from 200 client businesses. They want to determine how the businesses compare among four variables: 2015 Profit in millions of dollars 2016 Profit in...

Excel File Edit View Insert Format Tools Data Window Help Mon Nov 8 6:52 PM ... AutoSave OFF A9FvG... CC6582 Home Insert Draw Page Layout Formulas Data Review View Tell me Share Comments Insert C...

Instructions Fill out the questions in the pictures below. Copy of Grayson Dotson - [Template] ExpGrowthDecaySE * @ Saving- 6 Share G File Edit View Insert Format Tools Add-ons Help Last edit was...

need total summary with result on this paper GANIT J. Bangladesh Math. Soc. (ISSN 1606-3694) 34 (2014) 75-87 SUPPLY CHAIN OPTIMIZATION BY MIXED INTEGER PROGRAM FOR MANUFACTURER AND RETAILER SYSTEM OF...

ABC Hardware Store had the following transactions during the year starting January 1, 2020. At the beginning of 2020, the ledger of ABC showed Cash of 5,000 SR, opening inventory 3000 SR (300 units...

Hello, I need assistance to complete the attached assignment. Chapter 3: Project 3 Chapter 4: Project 4 ##################>### #############################V########################### ### ###T###...

I need help with C++ HW. Write a program to play a peg jumping game where the objective of the game is to leave the fewest number of pieces on the board possible. There are solutions that end up with...

Amran is a successful sole proprietor in Kuala Lumpur dealing in business of Italian furniture. He is thinking to expand the business after many potential vendors indicate interest to sell the...

What advice would you want to give to a person who is planning to convert the manufacture of a component from die casting to powder metallurgy?

b . Would John Deere's finance and interest income be treated as operating or nonoperating?

PRINTER VERSION

Pay him, do not wait until I sign

Tell what you mean without sounding too dominant, i.e. show authority without sounding instructive

Speak clearly and distinctly with moderate energy